第1966题:椭圆的渐屈线
[定义]
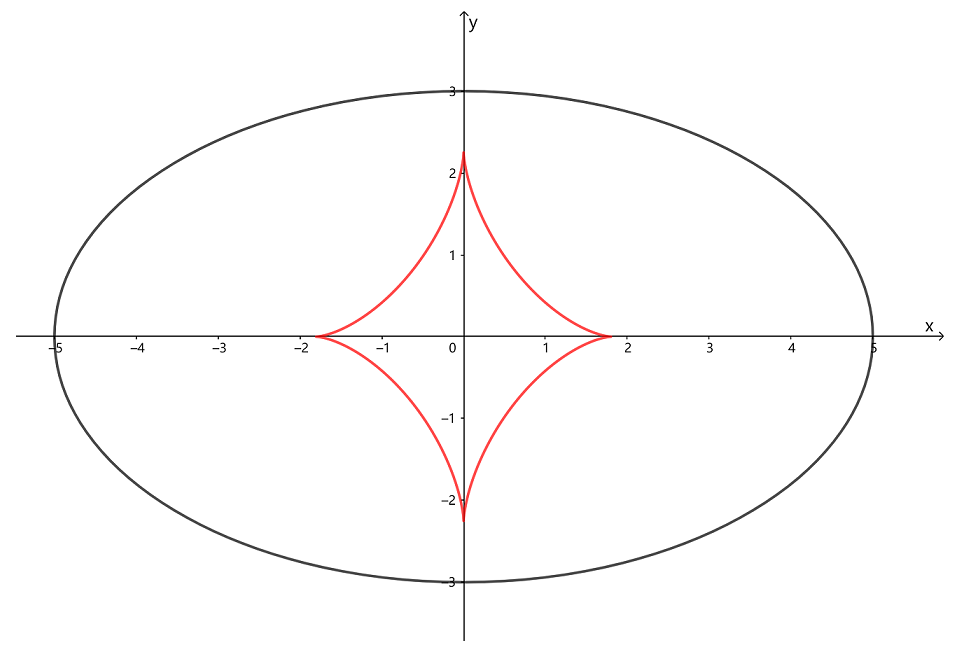
当动点在曲线上运动时,动点所在位置的曲率中心(曲率圆的圆心)形成的轨迹称为渐屈线. 如下图,椭圆的渐屈线类似星星,也称为星形线.
渐屈线计算公式
⎩⎪⎪⎨⎪⎪⎧α=x−y′′y′(1+y′2),β=y+y′′1+y′2 .
[题目]
用椭圆的参数方程
{x=acosθ,y=bsinθ
计算椭圆的渐屈线参数方程.
[解]
dθdx=−asinθ , dθdy=bcosθ
所以
y′=dxdy =dx/dθdy/dθ =−abcotθ
y′′=dx2d2y =dθdxdθd(dxdy)
=asinθab(−csc2θ)
=−a2sin3θb
于是有
y′=−asinθbcosθ
y′′=−a2sin3θb
代入渐屈线计算公式得到
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧α=acosθ−−a2sin3θb−asinθbcosθ(1+(−asinθbcosθ)2),β=bsinθ+−a2sin3θb1+(−asinθbcosθ)2
={α=___,β=___
(以下选项中,c2=a2−b2 )
A. ac2cos3θ,−bc2sin3θ
B. −ac2cos3θ,bc2sin3θ
C. bc2cos3θ,−ac2sin3θ
D. −bc2cos3θ,ac2sin3θ


 安卓手机扫描二维码安装App
安卓手机扫描二维码安装App
 苹果手机扫描二维码安装App
苹果手机扫描二维码安装App