第1437题:圆锥曲线的一些二级结论
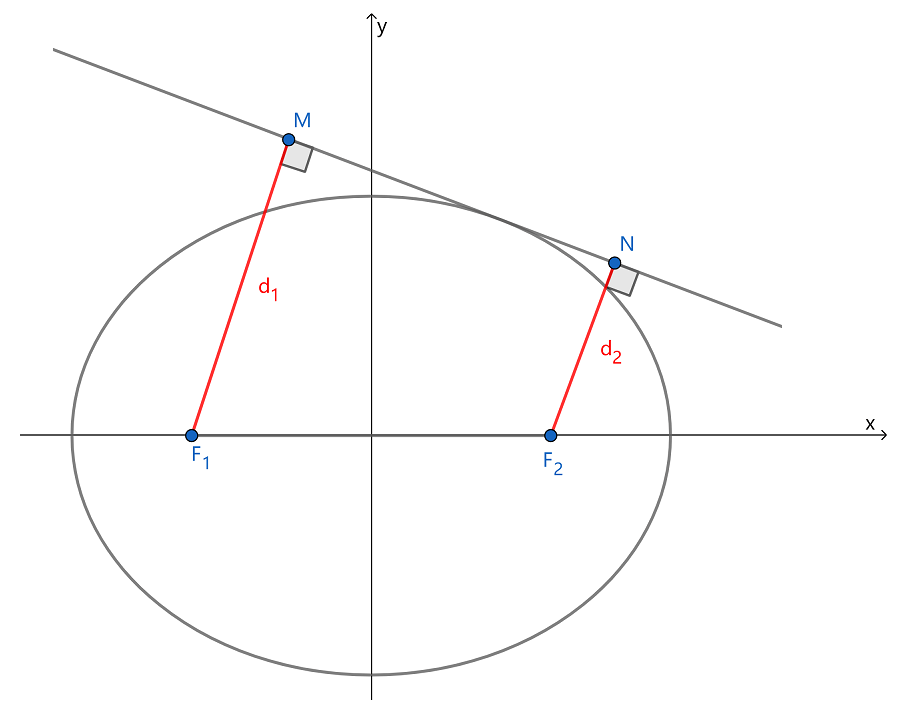
如图,直线 与椭圆 相切, 是椭圆的两个焦点, 分别是两个焦点到切线的距离,则 等于( ).
A.
B.
C.
D.
提示:设出切点得到切线方程,计算两个焦点到切线的距离.

 安卓手机扫描二维码安装App
安卓手机扫描二维码安装App第1437题:圆锥曲线的一些二级结论

如图,直线 与椭圆 相切, 是椭圆的两个焦点, 分别是两个焦点到切线的距离,则 等于( ).
A.
B.
C.
D.
提示:设出切点得到切线方程,计算两个焦点到切线的距离.
 苹果手机扫描二维码安装App
苹果手机扫描二维码安装App