第1521题:旋转矩阵
如图,点 P 与坐标原点的距离是 r ,与 x 轴正向的夹角为 θ ,将点 P 逆时针旋转 α 角度得到 P′ 点,由此我们可以得到两个方程
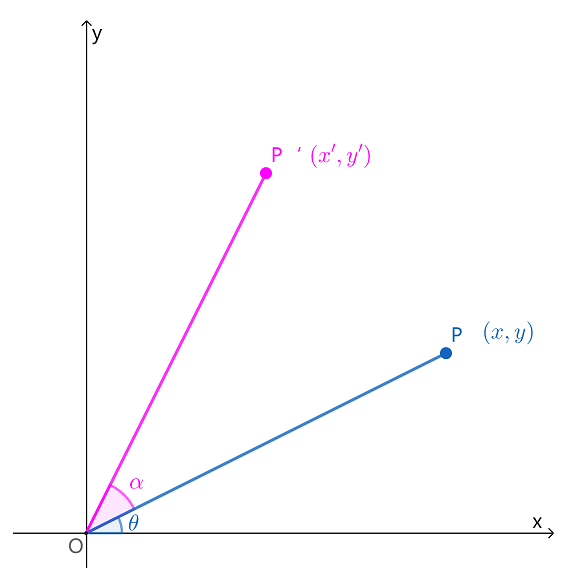
{x=rcosθ,y=rsinθ
{x′=rcos(θ+α),y′=rsin(θ+α)
由两角和的三角函数公式
sin(α±β)= sinαcosβ± cosαsinβ
cos(α±β)=cosαcosβ∓ sinαsinβ
得
{x′=xcosα−ysinα,y′=xsinα+ycosα
于是我们得到平面中点绕原点旋转矩阵
[cosαsinα−sinαcosα]
根据此矩阵计算,如果将平面中的点 (1,√3) 逆时针旋转 6π ,得到点的坐标是( ).
A.(2,2√3)
B.(21,2)
C.(2√3,2)
D.(0,2)
此旋转变换公式在计算机图形学中应用非常广,建议保存以备查询.


 安卓手机扫描二维码安装App
安卓手机扫描二维码安装App
 苹果手机扫描二维码安装App
苹果手机扫描二维码安装App