第240题：看成整体

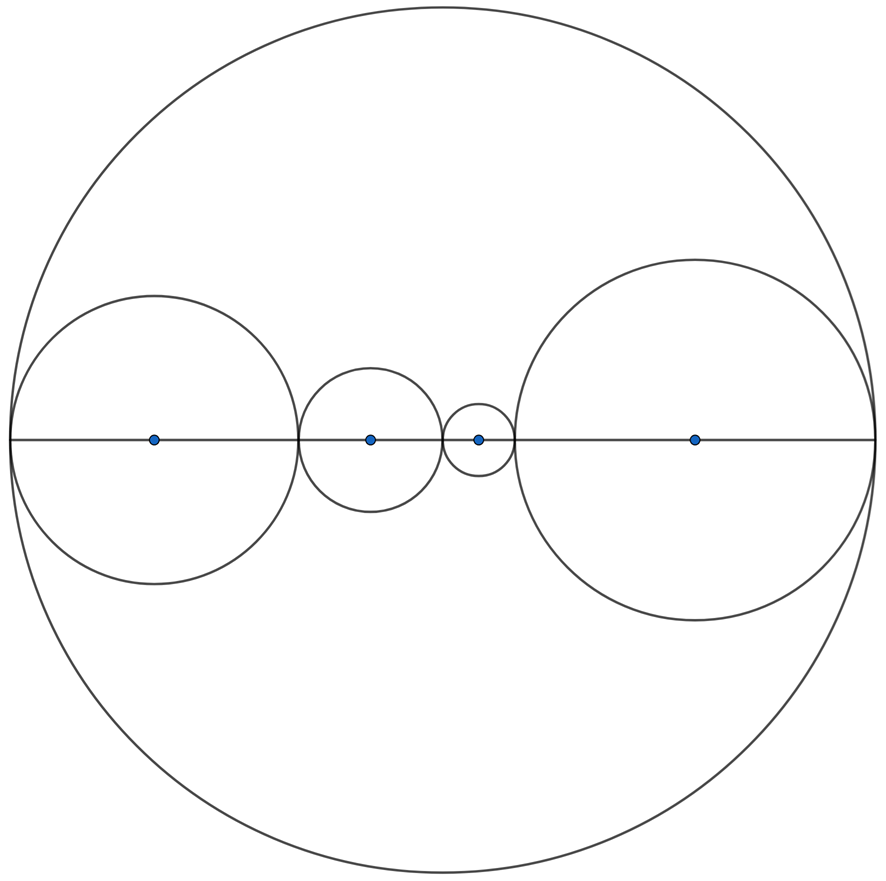
如下图，直径为12的大圆中有4个紧挨（相切）着的小圆，小圆的圆心都在大圆的同一个直径上，求4个小圆周长的和是多少。

1995年，三位数学家——大卫●贝里、彼得●波温、西蒙●普劳夫，发现了一个有关$\pi$ 的全新公式，这是第一个能够自我修正的$\pi$ 的公式，就是说，如果你在计算第367位时犯了错误，你后面的计算依然有效。

这个公式叫做 Bailey-Borwein-Ploffe 公式，如下：

$\pi=\displaystyle\sum_{k=0}^{\infty}\lbrack \dfrac{1}{16^k} (\dfrac{4}{8k+1}-\dfrac{2}{8k+4}-\dfrac{1}{8k+5}-\dfrac{1}{8k+6})\rbrack$

这是一个基于十六进制的公式，对十进制计数不起作用。

十六进制的$\pi$ 的前几位是

$\pi=3.243F6A8885A308D3\cdots\cdots$ ，其中A至F代表数字10至15，它们在十六进制中是单数位。

上面公式显示不完的话，看这个图