第753题:解直角三角形
在,和均为锐角,, ,且,则 的值为( ).
A. B.
C. D.
A明显不对,因为根据定义cos A 等于邻边比斜边,而直角三角形中,斜边必大于邻边,所以\cos A必小于1. 正弦同理.
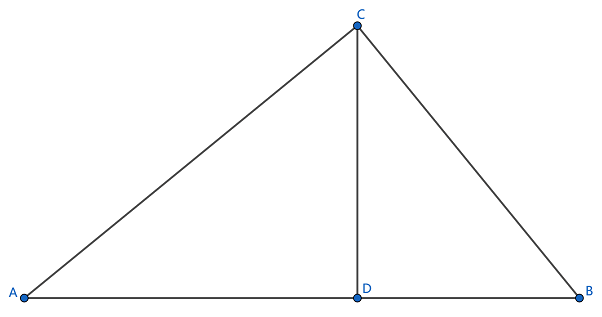
图中辅助线已做出, ,本题有提示.

 安卓手机扫描二维码安装App
安卓手机扫描二维码安装App第753题:解直角三角形
在,和均为锐角,, ,且,则 的值为( ).
A. B.
C. D.

A明显不对,因为根据定义cos A 等于邻边比斜边,而直角三角形中,斜边必大于邻边,所以\cos A必小于1. 正弦同理.
图中辅助线已做出, ,本题有提示.
 苹果手机扫描二维码安装App
苹果手机扫描二维码安装App