第1874题:高阶导数的应用
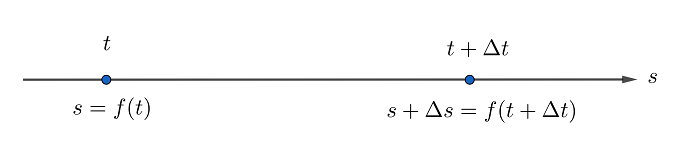
如上图,设物体的位置 是时间t的函数 ,则从 到 时间内物体的平均速度为
时刻的速度(瞬时速度)是位置关于时间的导数
时刻的速率是速度的绝对值
速率
加速度是速度的变化率,即速度关于时间的导数
加速度的突然改变,即加速度变于时间的导数称为急推(jerk)
自由落体运动符合以下函数
,其中 是重力加速度,那么自由落体的急推是多少?

 安卓手机扫描二维码安装App
安卓手机扫描二维码安装App第1874题:高阶导数的应用
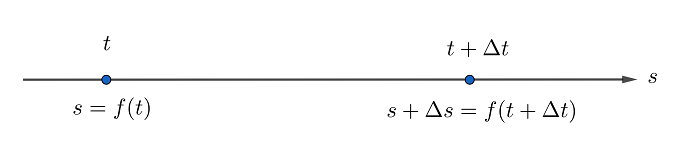
如上图,设物体的位置 是时间t的函数 ,则从 到 时间内物体的平均速度为
时刻的速度(瞬时速度)是位置关于时间的导数
时刻的速率是速度的绝对值
速率
加速度是速度的变化率,即速度关于时间的导数
加速度的突然改变,即加速度变于时间的导数称为急推(jerk)
自由落体运动符合以下函数
,其中 是重力加速度,那么自由落体的急推是多少?
 苹果手机扫描二维码安装App
苹果手机扫描二维码安装App