第1393题：圆锥曲线切点弦的方程

再继续观察，过圆锥曲线外一点 $(x_0,y_0)$ 向圆锥曲线引两条切线，切点分别为$A,B$ ，直线 $AB$ 的方程：

在椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ 上弦 $AB$ 的方程为 $\dfrac{x_0x}{a^2}+\dfrac{y_0y}{b^2}=1$

在双曲线 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ 上弦 $AB$ 方程为 $\dfrac{x_0x}{a^2}-\dfrac{y_0y}{b^2}=1$

在抛物线 $y^2=2px$ 上弦 $AB$方程为 $y_0y=2p(\dfrac{x_0+x}{2})$

在抛物线 $x^2=2py$ 上弦 $AB$方程为 $x_0x=2p(\dfrac{y_0+y}{2})$

在圆 $x^2+y^2=r^2$ 上弦 $AB$方程为 $x_0x+y_0y=r^2$

于是，柯西又得到一个结论，即过圆锥曲线外一点做的曲线两条切线，两切点间弦的方程可以这样得到：

1）把原方程中的 $x^2$ 替换成 $x_0x$ ，原方程中的 $y^2$ 替换成 $y_0y$ ;

2）把原方程中的 $x$ 替换成 $\dfrac{x_0+x}{2}$ ，原方程中的 $y$ 替换成 $\dfrac{y_0+y}{2}$ ;

3）得到的新方程即两切点间连线的方程.

柯西的结论对吗？

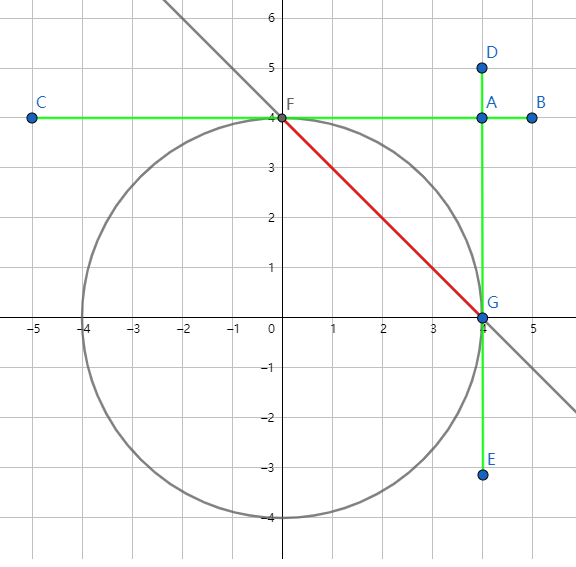
如上图，圆的方程为 $x^2+y^2=16$ ，过圆外一点 $A$ 做圆的两条切线，可以快速得到切点弦 $AG$ 的方程 $x+y=4$ .