第1885题:参数方程的求导
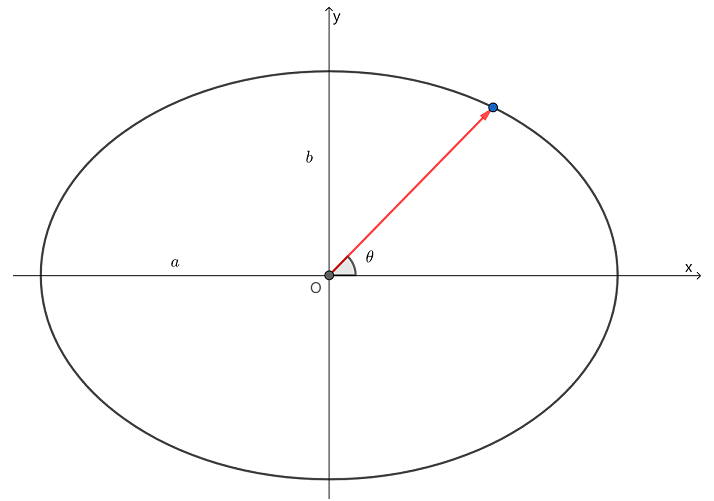
已知椭圆的参数方程为
其中角度 为参数, 为半长轴的长度, 为半短轴的长度,如上图. 则此椭圆在 角处切线的斜率是( ).
A.
B.
C.
D.

 安卓手机扫描二维码安装App
安卓手机扫描二维码安装App第1885题:参数方程的求导

已知椭圆的参数方程为
其中角度 为参数, 为半长轴的长度, 为半短轴的长度,如上图. 则此椭圆在 角处切线的斜率是( ).
A.
B.
C.
D.
 苹果手机扫描二维码安装App
苹果手机扫描二维码安装App