第1076题：构造三角形证明不等式

上一题

先给出上题的一个简短证明：

由于 $x$ 是正整数，所以有

$x^2$ $< x^2+x+1$$<x^2+2x+1$$=(x+1)^2$

所以，$x^2+x+1$ 界于两个相邻整数的平方之间，$x$ 和 $x+1$ 之间不可能再有别的整数了，得证。

补充下题中方框内缺失的符号.

题目

已知 $a,b,m$ 为正数，且 $a<b$ ，求证： $\dfrac{a}{b}<\dfrac{a+m}{b+m}$ .

分析

$\dfrac{a}{b}$ ，$\dfrac{a+m}{b+m}$ 的形式看起来很像相似三角形中对应线段成比例，所以联想到用相似三角形来证明.

证明

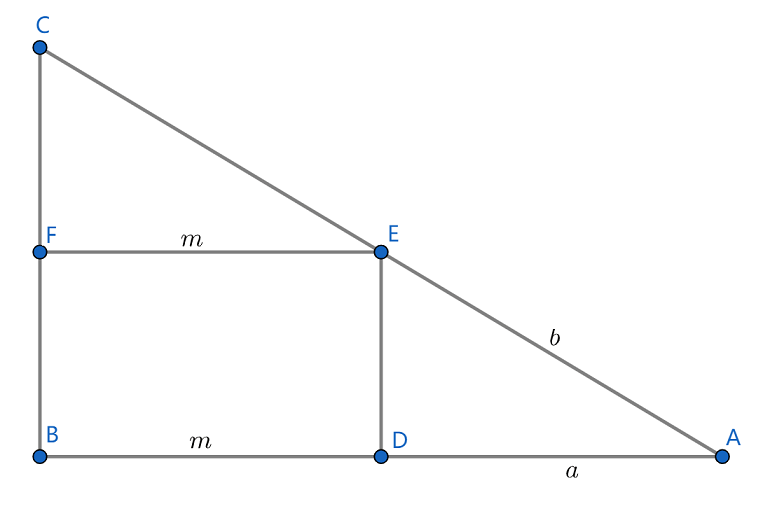
如图，在 $Rt \triangle ABC$ 的斜边上找一点 $E$ ，并过 $E$ 做两直角边的垂线，使得其中的

$AD=a$ ，$AE=b$ ，$DB=m$ ，显然有 $a<b$

且$\triangle ADE \thicksim \triangle ABC$

所以有

$\dfrac{AD}{AE}$ $\boxed{?}$ $\dfrac{AB}{AC}$ $= \dfrac{a+m}{b+CE}$ $<\dfrac{a+m}{b+EF}$ $\boxed{?}$ $\dfrac{a+m}{b+m}$

得证.