第1880题:隐函数的导数,齐次多项式
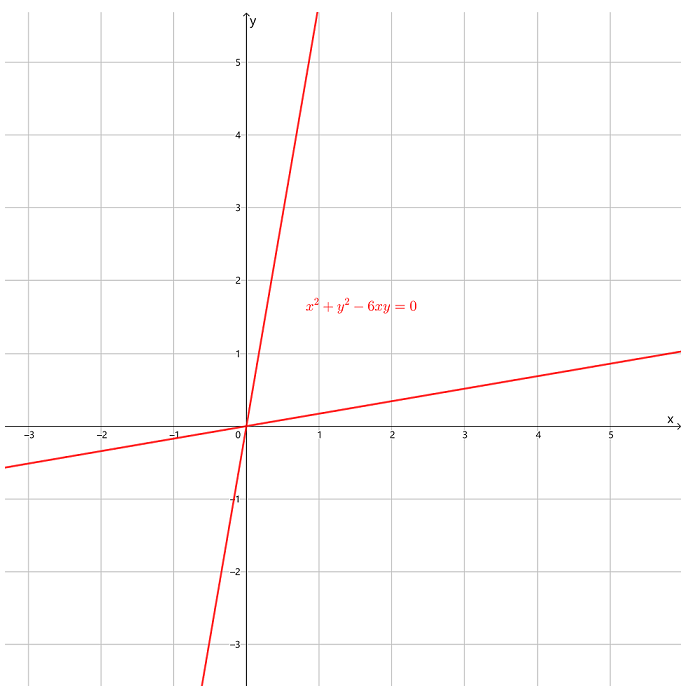
参考下图,继续做上一题,求由方程 所确定的隐函数的在 , 处的导数 , 是多少?
A. ,
B. ,
C. ,
D. ,

 安卓手机扫描二维码安装App
安卓手机扫描二维码安装App第1880题:隐函数的导数,齐次多项式
参考下图,继续做上一题,求由方程 所确定的隐函数的在 , 处的导数 , 是多少?
A. ,
B. ,
C. ,
D. ,

 苹果手机扫描二维码安装App
苹果手机扫描二维码安装App