第1959题:曲率半径
设有抛物线 , 则 , ,由曲率计算公式
得
可知当 , 时,即在抛物线的顶点处曲率最大且等于 .
如图,
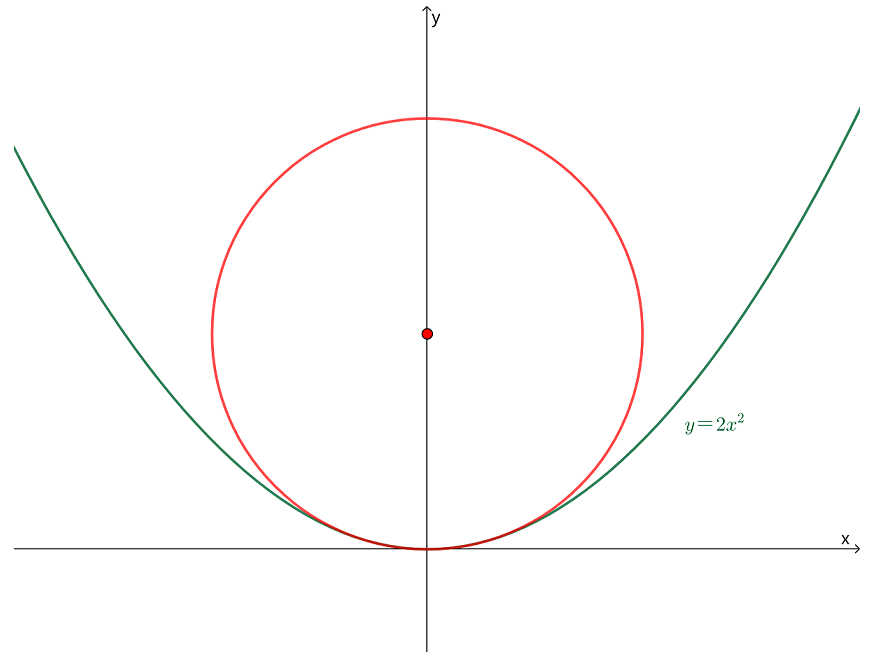
某工件内表面的截线为抛物线 ,现在要用砂轮磨削其内表面,为了在磨削时不使砂轮与工件接触处附近的那部分工件磨去太多,砂轮的半径应不大于抛物线上各点处曲率半径的最小值。本例中,砂轮的直径应为多大才合适?

 安卓手机扫描二维码安装App
安卓手机扫描二维码安装App第1959题:曲率半径
设有抛物线 , 则 , ,由曲率计算公式
得
可知当 , 时,即在抛物线的顶点处曲率最大且等于 .
如图,

某工件内表面的截线为抛物线 ,现在要用砂轮磨削其内表面,为了在磨削时不使砂轮与工件接触处附近的那部分工件磨去太多,砂轮的半径应不大于抛物线上各点处曲率半径的最小值。本例中,砂轮的直径应为多大才合适?
 苹果手机扫描二维码安装App
苹果手机扫描二维码安装App