第743题:通过相似三角形推导二次函数
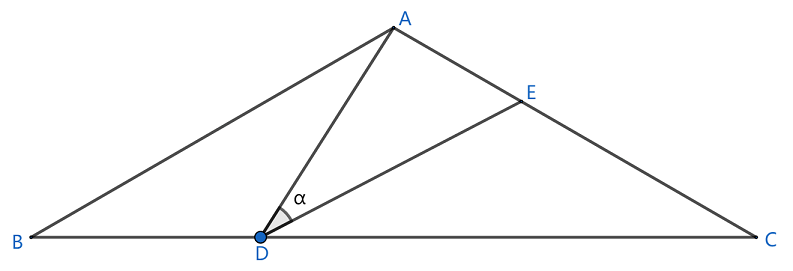
如图,在等腰三角形ABC中,,,点是边上的一个动点(不与、重合),在上取一点,使,可以得到 ,设,,则关于 的函数关系式是:
A.
B.
C.
D.
本题有提示.

 安卓手机扫描二维码安装App
安卓手机扫描二维码安装App第743题:通过相似三角形推导二次函数
如图,在等腰三角形ABC中,,,点是边上的一个动点(不与、重合),在上取一点,使,可以得到 ,设,,则关于 的函数关系式是:
A.
B.
C.
D.

本题有提示.
 苹果手机扫描二维码安装App
苹果手机扫描二维码安装App