第1537题：对称变换的逆变换

如图，对于正三角形，我们有以下对称变换集合

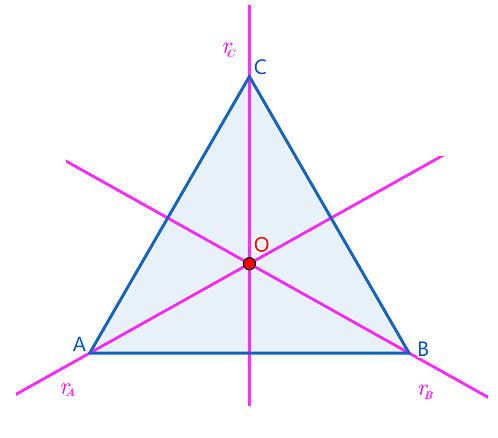
$D_3=$ { $I,r_a,r_b,r_c,\rho_1,\rho_2$ }

其中

$I$ 为恒等变换

$r_a$ 为关于对称轴 $r_a$ 所在直线的反射

$r_b$ 为关于对称轴 $r_b$ 所在直线的反射

$r_c$ 为关于对称轴 $r_c$ 所在直线的反射

$\rho_1$ 为以点O为中心作 $120\degree$ 旋转

$\rho_2$ 为以点O为中心作 $240\degree$ 旋转

如果一个变换 $a$ 与另一个变换 $b$ 的合成使得平面图形及图中各点位置没有改变，即两个变换的合成等于恒等变换 $I$

$a \cdot b =b \cdot a= I$

我们称 $b$ 为 $a$ 的逆变换（或 $a$ 为 $b$ 的逆变换），记作

$b=a^{-1}$ （或 $a=b^{-1}$ ）

那么，上图中的 $r_b$ 的逆变换 $r_b^{-1}$ 可能是以下哪些变换或哪些变换的合成？.

A. $r_b^{-1}=r_a$

B. $r_b^{-1}=r_b$

C. $r_b^{-1}=r_c$

D. $r_b^{-1}=r_a \cdot \rho_1$

E. $r_b^{-1}=r_b \cdot \rho_1$

F. $r_b^{-1}=r_c \cdot \rho_1$