第1315题：几何概型与经典概率问题

本题用几何概型求解一个经典的概率问题.

[题目]将长为L的一个木棒截为三段，求此三段小木棒能够构成三角形的概率.

[分析]设出所截三段的长度，将它们的取值范围平面上的区域表示出来，将问题转换为与面积有关的几何概型问题.

[解]

设事件M={三段构成三角形}

设所截出的两段长度分别为$x,y$ ，则第三段长度为$L-x-y$ .

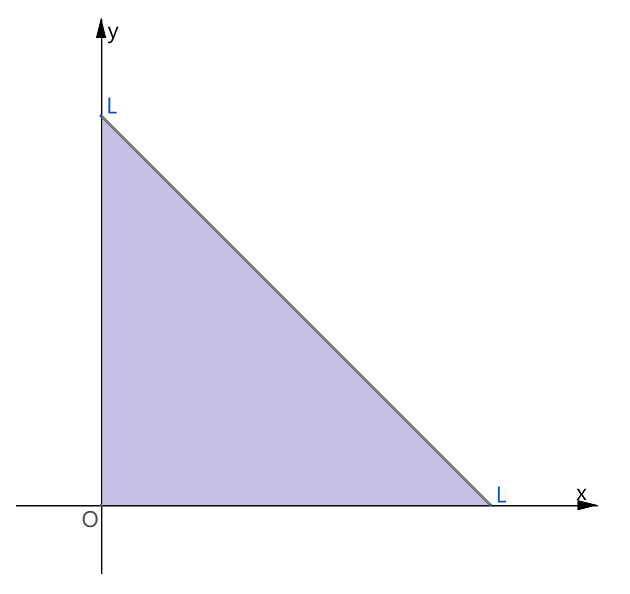
x和y的全部取值范围Q为：$0<x<L$ ,$0<y<L$ , $0<x+y<L$ ，它们在平面上构成下图中的淡紫色区域，即将木棒截成三段的所有可能的 $(x,y)$ 组合都将落在此淡紫色三角形区域内：

如果需要三段构成三角形，那么还需要满足：

$x+y>L-x-y$

$L-x-y+x>y$

$L-x-y+y>x$

解得事件M的取值范围为：$x<\dfrac{L}{2}$ ,$y<\dfrac{L}{2}$ ,$x+y>\dfrac{L}{2}$ ，它们在平面上构成下图中的紫色区域，即能组成三角形的所有可能的 $(x,y)$ 组合，都将落在此紫色三角形区域内：

那么

$P(M)=$$\dfrac{\text{M的面积}}{\text{Q的面积}}$ $=?$

A. $\dfrac{1}{2}$ B. $\dfrac{1}{3}$

C. $\dfrac{1}{4}$ D. $\dfrac{3}{5}$