第1440题:圆锥曲线一些二级结论
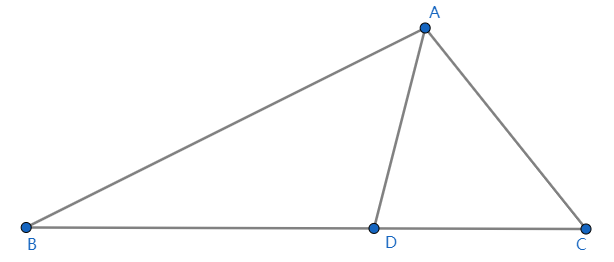
图1
如图1,我们知道,在 △ABC 中,如果 AD 是 ∠A 的角平分线,那么有:
S△ADCS△ABD=ACAB
S△ADCS△ABD=DCBD
DCBD=ACAB
根据以上三角形角平分线定理,如图2,在离心率为 e 的椭圆 a2x2+b2y2=1 中有焦点三角形 PF1F2 ,PN 是 ∠F1PF2 的角平分线,可以推导得出( ).
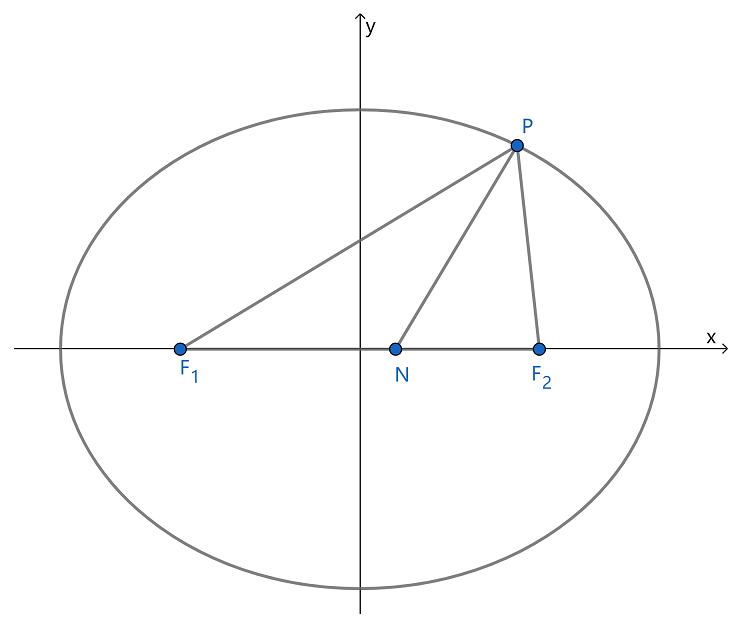
图2
A. PF1NF1=PF2NF2 =ba
B. PF1NF1=PF2NF2=ab
C. PF1NF1=PF2NF2 =e1
D.PF1NF1=PF2NF2 = e



 安卓手机扫描二维码安装App
安卓手机扫描二维码安装App

 苹果手机扫描二维码安装App
苹果手机扫描二维码安装App