第1824题:终极性态模型
定义:
对于数值很大的 ,我们有时候可以对复杂函数的性态用一个实际上以同样方式起作用的较为简单的函数作为该复杂函数的模型,并称其为原函数的终极性态模型.
当 时,称
是 的右侧终极性态模型,
当 时,称
是 的左侧终极性态模型.
例:
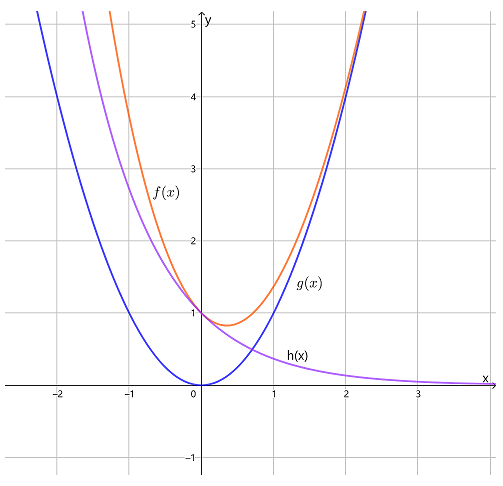
设 , 为其右侧终极性态模型, 为其左侧终极性态模型,则有( ).
A. ,
B. ,
C. ,
D. ,

 安卓手机扫描二维码安装App
安卓手机扫描二维码安装App第1824题:终极性态模型
定义:
对于数值很大的 ,我们有时候可以对复杂函数的性态用一个实际上以同样方式起作用的较为简单的函数作为该复杂函数的模型,并称其为原函数的终极性态模型.
当 时,称
是 的右侧终极性态模型,
当 时,称
是 的左侧终极性态模型.
例:
设 , 为其右侧终极性态模型, 为其左侧终极性态模型,则有( ).
A. ,
B. ,
C. ,
D. ,

 苹果手机扫描二维码安装App
苹果手机扫描二维码安装App