第1775题:渐开线
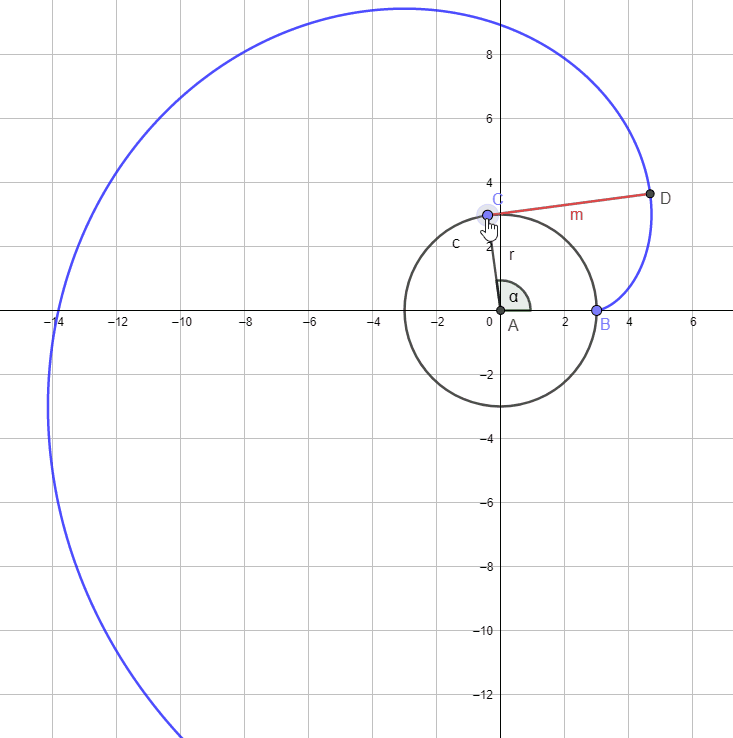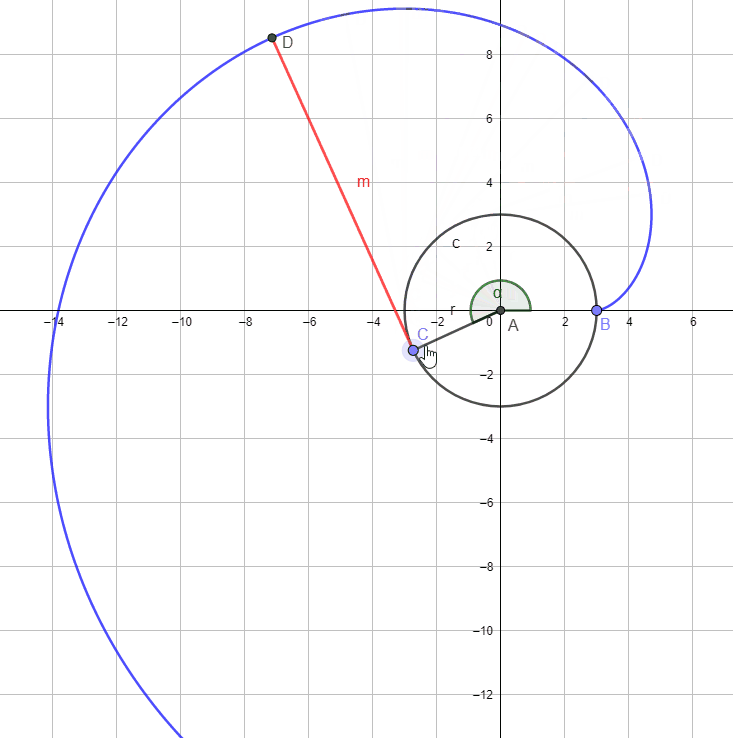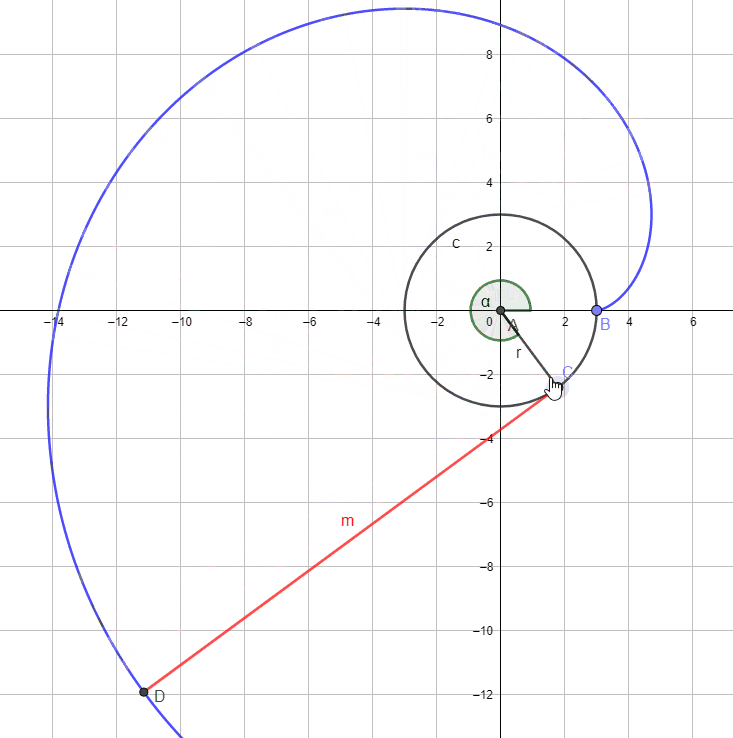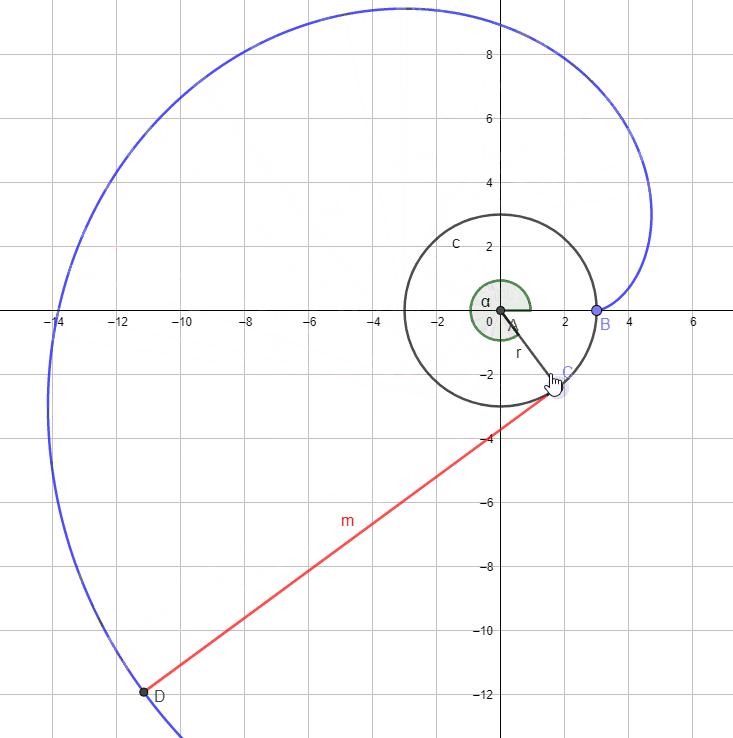
把一条没有弹性的细绳绕在一个圆盘上,在绳的外端系上一支笔,将绳子拉紧,保持绳子与圆相切而逐渐展开。我们把笔尖画出的曲线叫做圆的渐开线(involute),相应的定圆叫做渐开线的基圆(base circle).
如图,基圆的半径 r=3 ,由于绳子 M 是拉紧的,所以绳子与基圆相切,切点 C 转过的角度为 α ,则渐开线的参数方程为( ).
A.{x=3(cosα+αsinα)y=3(sinα−αcosα)
B.{x=4(cosα+αsinα)y=4(sinα−αcosα)
C.{x=5(cosα+αsinα)y=5(sinα−αcosα)
D.{x=6(cosα+αsinα)y=6(sinα−αcosα)


 安卓手机扫描二维码安装App
安卓手机扫描二维码安装App
 苹果手机扫描二维码安装App
苹果手机扫描二维码安装App