第1040题:两角和的余弦公式
cos75°=?
A. 4√6−√2
B. 4√6+√2
C. 4√5−√2
D. 4√5+√2
75=30+45.
用上一题中的图记公式太复杂了,下图用向量方式记忆:
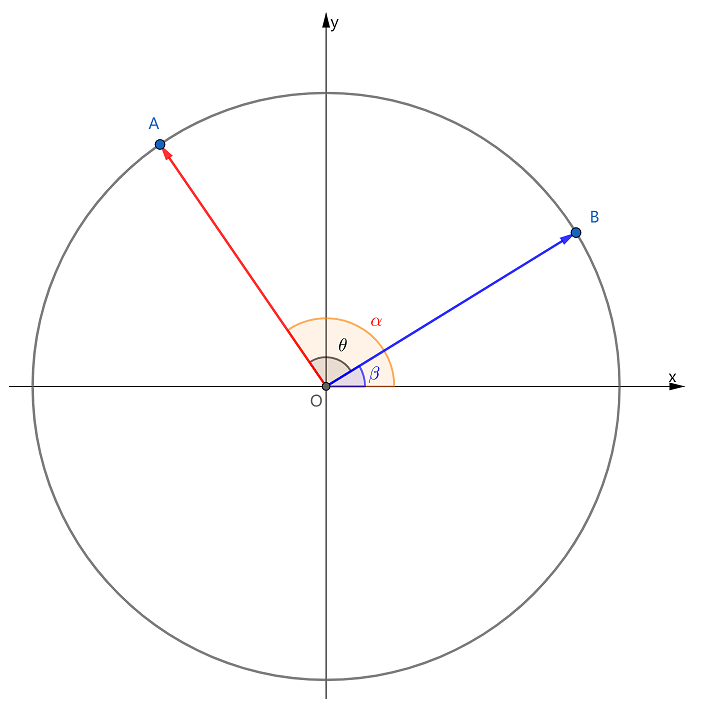
OA=(cosα,sinα)
OB=(cosβ,sinβ)
OA⋅OB
=(cosα,sinα)⋅(cosβ,sinβ)
=cosαcosβ+sinαsinβ
cos(α−β)=cosθ
cos(α+β)=cos(α−(−β))


 安卓手机扫描二维码安装App
安卓手机扫描二维码安装App
 苹果手机扫描二维码安装App
苹果手机扫描二维码安装App