广义相对论中的微分几何引论2

广义相对论研究非平直的连续时空，微分几何则是描述它的数学结构，一般情况下，欧几里得空间不再适用，反之，用各种各样的流形，流形是局部的欧几里得空间：

举例说一个球面就是一个流形，因为观察小三角形，他的内角和等于 $180\degree$ ，以及其它一些满足欧几里得空间的性质，然而大三角形则不同，这个三角形每个角都是 $90\degree$ ，内角和是 $270\degree$ ，于是不同于欧氏几何，球面是局部欧几里得空间，地球表面也是一个流形。

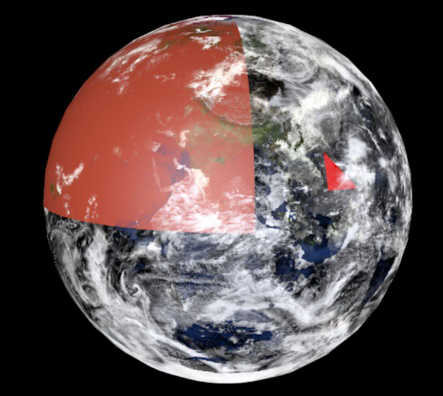
有些人会问，红色部分不是三角形，然而这时站在欧式空间上说的，在非平直的空间上，或者说一个拓扑空间，这些三角形看上去只是变形了而已。

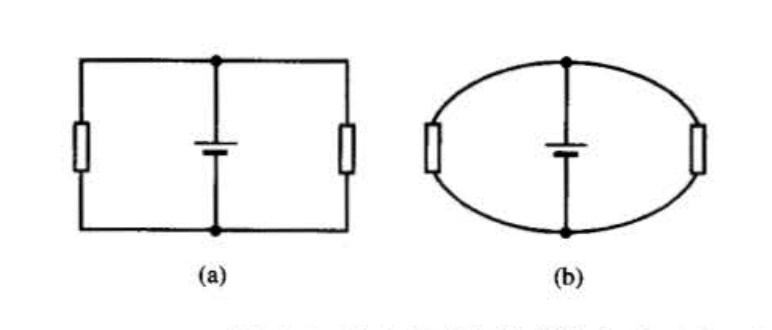
可以看出，这三个三角形之间存在映射，使得前一个三角形的点对应后一个三角形的点。实际上，上图三个三角形在数学上称为同胚，同胚的意思是说：两个流形，把其中一个弯曲，延展，变形，剪切（剪开后必须最后需要沿着剪开的部分完美缝合）变成另一个，则认为二者同胚，换言之：你可以将上图任意一个三角形捏成另一个，所以有人说：拓扑学是橡皮膜上的几何学。与度量空间不一样的是不需要大小，距离概念。研究这些问题需要的是一个拓扑空间。读者或许会思考，什么样的问题竟然不需要定义距离，举个例子，在下图电路中，a，b同胚，这样一个电路，在设计时无需考虑电线之间的长度。

又比如拓扑学中经典的七桥问题：

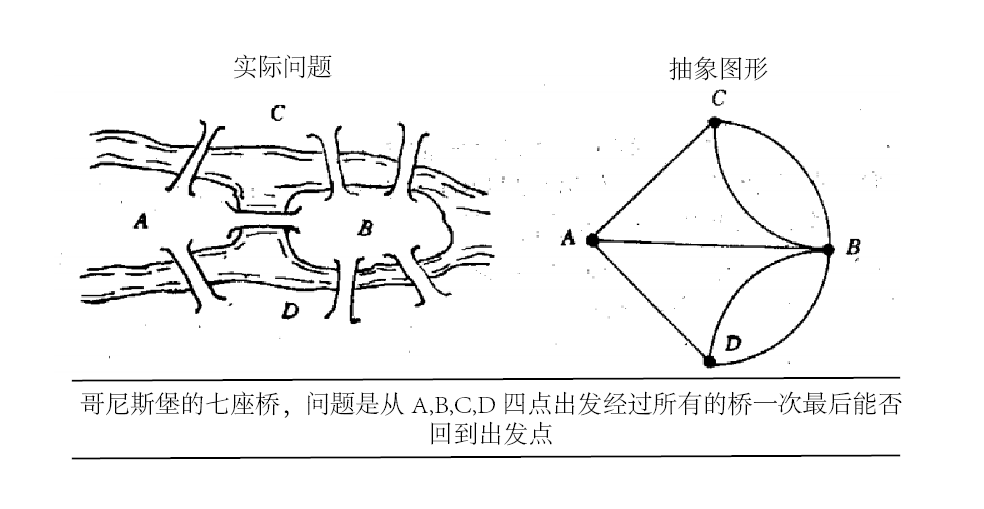
哥尼斯堡的居民如何尝试均没有成功，而因为走法一共有5040种，在没有尝试所有方法之前，谁也不能说这桥走不通，欧拉将实际问题抽象成上图的图形，不但彻底解决此问题，还开创了图论的先河，这类问题抽象成几何图形时，根本无需考虑其中任一两点的距离，又有读者会问，如果问题变成从A点走到B点的最短路程，使之成为最短路径问题，是否又回到度量空间了，答案是不需要，因为任何一条路的距离数值可以被另外记录下来，或者称之“权”，给定道路一数值后称之为“加权”，读者若对七桥问题的证明感兴趣可以在数学长征中搜索【七桥问题】。

以本题为例：证明任一开区间 $(a,b) \in R$ 与 $R$ 同胚。

尽管这是一个不证自明的习题，但是我们先来考虑下，开区间 $(a,b)$ 是否存在一个映射， 将区间 $(a,b)$ 的每个点映射到 $R$ 上？通过上期内容不难想象到下图：

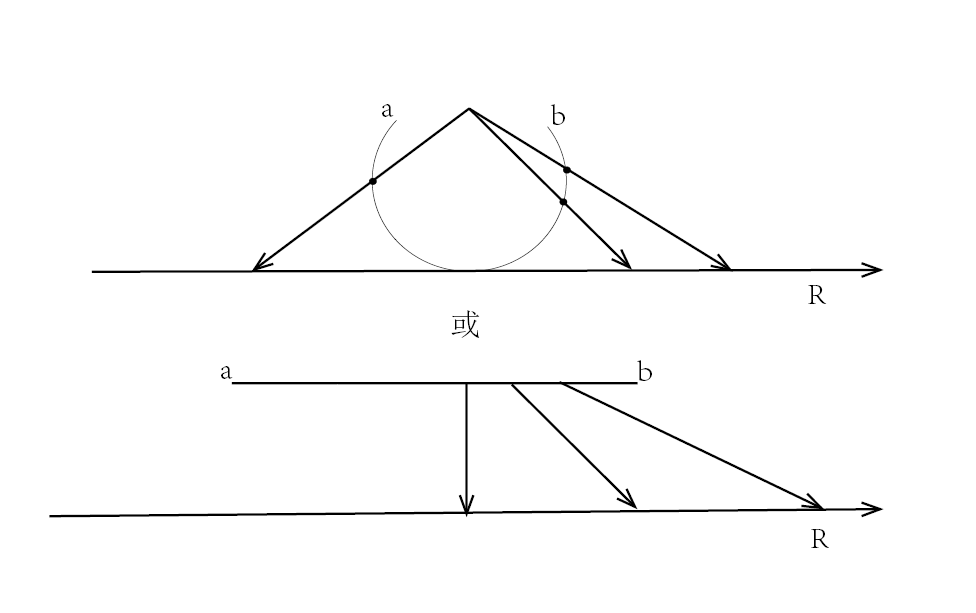
或者类似的映射。那么开区间 $(a,b)$ 能否弯曲，延展，变形，剪切变成R呢，这很好操作，将 $(a,b)$ 延展即可，通俗的说，用两只手捏住$a$ ，$b$ 两端，然后拉长，最后即可变成 $R$ ，$(a,b)$ 是开集正好对应 $R$ 集的 $\infty$ 处。

下面给出同胚的定义：若 $\exists$ 映射 $f: x \rightarrow y$ ，满足：$(a)f$ 是一一到上的；$(b)f$ 及 $f^{-1}$ 都连续,我们称拓扑空间 $(x, \mathscr {T})$ 和 $(Y, \mathscr {S})$ 互相同胚，将 $f$ 称为同胚映射，简称同胚。

可以看出，这里的背景不再是欧式空间，我们从欧式空间或者度量空间切换到不考虑大小距离的拓扑空间，这需要为拓扑空间下定义。定义：非空集合 $X$ 的一个拓扑 $\mathscr {T}$ 是$X$ 子集的集合，其中的元素称为开集，并且满足：

(a) $X,\varnothing \in \mathscr {T}$ ;

(b) 若 $O_i \in \mathscr {T}$ , $i=1,2,3, \cdots, n$ ，则 $\displaystyle\bigcap_{i=1}^n O_i \in \mathscr {T}$ ;

(c) $\mathscr {T}$ 中任意有限或无限集合 $O_a$ , 有 $\displaystyle\bigcup_{a} O_a \in \mathscr {T}$ .

看上去像集合的集合，我们举个例子： $X={1,2,3}$ ，则

$\mathscr {T}=$ {$\varnothing$ ,{1},{2},{3},{1,2},{2,3},{1,3},{1,2,3}}

是它的一个拓扑。

$\mathscr {T}=$ {{1},{3},{1,2},{1,3}}

也是它的一个拓扑。元素最多的拓扑（全部子集的集合）又叫离散拓扑，元素最少的拓扑又叫做凝聚拓扑，还以上者为例，

$\mathscr {T}=$ { $\varnothing$ ,{1},{2},{3},{1,2},{2,3},{1,3},{1,2,3}}

为X的离散拓扑,

$\mathscr {T}=$ { $\varnothing$ ,{1,2,3}}

为X的凝聚拓扑。

今天就先到这里，下一期预告：覆盖与图册