青羽讲数学史（四）上

青羽讲数学史（四）

中国篇上·古中国璀璨的数学成就

数学长征，青羽

1.炎黄纪——鸿蒙太初诞生的灵智

同所有文明诞生之初一样，我们的先民从野蛮走向文明的漫长历程中，逐渐认识了数与形的概念。在古时，数学仅有算数和几何两大分支，算数主要用来进行天文记历、测算山高谷深、计算粮食产量、栗米交换，几何知识则主要用于丈量土地面积，建筑、工具的制造等。

传说伏羲创造了画圆的“规”、画方的“矩”，而黄帝臣子倕是“准绳”的创始人。这规矩准绳便是我们祖先使用最早的数学工具，早在大禹治水时，禹便“左准绳，右规矩。”——《史记·禹本纪》

在我国古来的著作《易经系辞传》中，有一句话是：“河出图，洛出书，圣人则之。”这里所说便是我国古代数学发明的一个瑰宝——河图洛书，文中的圣人指伏羲式。

河图中的黑点表示阴数（偶数），白点表示阳数（奇数），各线上点的个数代表一个数字。图中数字共三层，最外层四数之和为30，中层四数之和为10，内层三数之和为15，三数相加为55。30、10、15均为5的倍数，说明了以5为中心。图中1至9的数中除5以外都是不重复的数字，唯有5有3个，如果把其中两个5合并为10，那么有1至10的和为：1+2+3+4+5+6+7+8+9+10=55.这是等差数列前n项和的最典型例子。

洛书则把1至9着9个数字摆成方阵，并且以5为中心。此图中任意一行，任意一列及两条对角线上的数字之和都是15，对于满足这种性质的数阵，又称之为幻方。

别看河图洛书的内容这么简单，中国学者在两千年的时间里，都对其争议不断。可以说，河图和洛书是华夏文明之源、阴阳五行术数之根，各类纷繁复杂的中国古代术数莫不以河图洛书为理论基础。某种程度上说，河图洛书反映出中国人对数字的崇拜和时空观念。与古希腊提出“万物皆数”的毕达哥拉斯一样，对数字的崇拜是世界上各个名族在文化启蒙之初的共同特征。

此外，在漫长的中国历史中，对河图洛书的研究从未停止。因为河图洛书与八卦文化异形而同源。在《易经·系辞下》有记载：“古者包牺氏之王天下也，仰则观象于天．俯则观法于地．观鸟兽之文，与地之宜，近取诸身，远取诸物，于是始作八卦．以通神明之德，以类万物之情。”这描述的是伏羲氏创八卦的内容，可见八卦是伏羲观天法地而创，其内容必囊括天地之理数，即以数为载体，尽述天地之理。这与毕达哥拉斯的观念何其相似！

在未有科学时代，理学是中国学者所研究的热门内容。理学即可解释天地阴阳五行等自然事物，又记述心法、修养、处世等人文之道，在中国古代是最为完备的理论体系。我曾拜读陈抟老祖所作的《河洛理数》一书，看似可以八卦推算命运、玄奥莫测又有一定的信服力。虽然我对这满篇玄文一字不通，但仍可感先哲之智慧。在现代观念下，理学已难以被理解，但在古时它被我们的先民奉为至高无上的科学。

与河图洛书相同的还有八卦文化。古人总结自然界万物的规律，认为万物均由天地阴阳交感而成，形成无极生太极，太极生两仪，两仪生四象，四象生八卦，八卦化万物的美学观。

图为哥本哈根学派标志，阴阳图与波尔的“对立即互补”思想极为贴切

八卦图发展至今，已经越来越收中外学者的重视。如量子力学的哥本哈根学派以八卦图作为他们学派的标志，韩国以八卦图作为他们的国旗，这都说明八卦图具有超凡脱俗的美感。

2.春秋战国——百家争鸣中促成的数学体系

除了河图洛书与八卦外，在商周时，算术学已比较成熟。在公元前一世纪，《周髀算经》中就记载了勾股定理，以及如何计算天文历法，揭示日月星辰的运行规律等。并且此时无论是统治者还是思想家，都认识到了数学的重要性，由此西周学者将“数”作为“六艺”之一，使所有贵族子弟学习。

到了春秋时期，筹算已得到普遍的应用。战国时期的百家争鸣也促进了数学的发展，思想家们开始争论一些直接与数学有关的命题。例如我们之前说到的道家学派《庄子·天下篇》的命题“一尺之棰，日取其半，万世不竭。”墨家学派就不同意此命题，认为将一线段不断地分割，最终必然会出现一个不可再分割的点。道家学派论述了有限长度可分割成一个无穷序列，墨家的命题则指出这种无限分割的变化和结果。

这种争论持续了数百年，最终确立了一些命题，使得筹算学得到了一定的公理基础。但事实上，人们并没有如古希腊那般公理化的思想，这里的公理基础只是代表所有人都认可的命题。

及秦始皇立，这种学术之风几乎被瓦解。到了汉朝，至汉武帝“罢黜百家，独尊儒术”后，儒家成为思想意识形态的一极，后世无非是对它进行修修补补。然而，物极必反。没有了百家争鸣的局面，单一的思想模式造就的政治法律文化等，无非就是专制。于这种专制统治下，中国数学思想的发展，也就可以得见尽头了。

但是，在东汉时期，《九章算术》的横空出世可谓是晴天霹雳。它总结了战国至秦汉时期的数学成就，其内容还有“盈不足术”、方程思想、求图形面积、体积等方法。它还包含世界上最早的完整的线性方程组的解法、最早引用负数。可以说，《九章算术》确立了中国古代数学的框架，以计算为中心，密切联系实际。

《九章算术》不仅在后世近两千年的时间里作为中国历朝的贵族子弟的数学教材，还传至印度、阿拉伯、日本、朝鲜等国家，甚至通过这些地区远至欧洲，其影响力可见一般。有人说，《九章算术》之于东方，有如《几何原本》之于西方，这东西两颗明珠交相辉映，代表了两方数学体系的成熟。

但即使如此，《九章算术》仍有不容忽视的缺 点：没有任何数学概念的定义，也没有给出任何推导和证明。到了魏晋时期，刘徽给《九章算术》作注，才大大弥补了这个缺陷。

3.魏晋朝——诘辩求胜中极速发展

魏晋时期出现的玄学，不为汉儒经学所束缚，思维比较活跃，从而跳脱出旧时数学笼统的思维框架，数学家得而能够更加辩证地看待那些已知的数学定理。

刘徽是中国杰出的数学家，在举世追崇道法玄学、寻求长生秘法的魏晋时代，刘徽独尽毕生之力钻研数学之道。他的“割圆术”首次将极限思想用于数学证明中，“割圆术”即在圆内做一个正n边形，不妨设圆半径为1，由于当n越来越大时，正n边形的面积就越来越趋近于圆的面积。

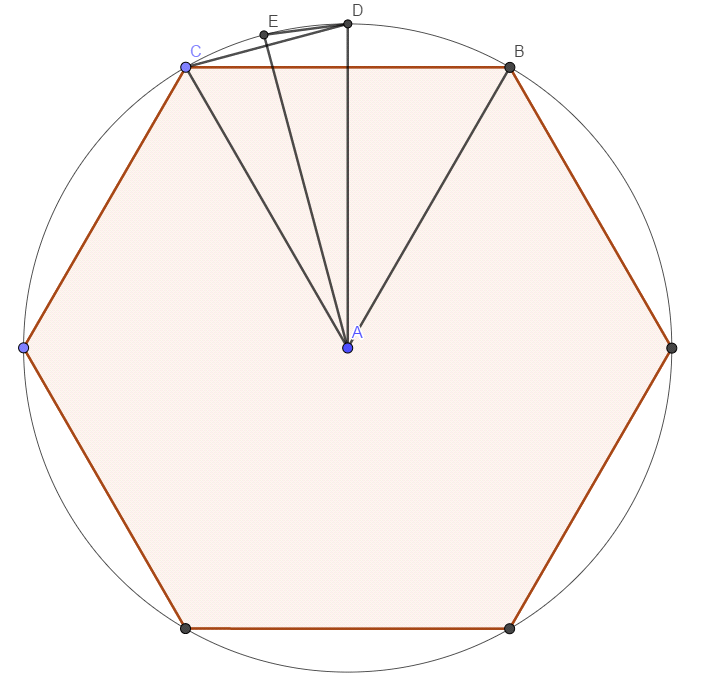
那么我们不妨沿着刘徽的思路进行一次尝试。

令 $r=1$ ，则 S_圆 $= \pi r^2 = \pi$

用 $S_n$ 表示正边形的面积，有 $\pi \approx S_n$

则 $S_6=6 S_{\triangle ABC}$

$=6 \times \dfrac{1}{2} \times 1 \times 1 \times sin 60 \degree$

$=3 sin 60 \degree$

同理

$S_{12}=12S_{\triangle ACD}$

$=12 \times \dfrac{1}{2} \times 1 \times 1 \times sin 30 \degree$

$=6 sin 30 \degree$

$S_{24}=24S_{\triangle ADE }=12 sin 15 \degree$

通过计算，可得到

$S_6 \approx 2.598$ ，$S_{12} =3$ ，$S_{24} \approx 3.106$

我接下来画一个圆内接正24边形。

可以看到，即使圆内接正24边形的图形看起来已经和圆没多大区别，但如果仅它的面积仍只能近似到π的小数点后1位。

如果我们想要计算正48边形面积，用类似的方法会有一个问题

即 $S_{48}=24 sin 7.5 \degree$ ，如何计算 $sin 7.5 \degree$ 的值呢？

这时我们可以利用到

$sin \dfrac{x}{2} = \sqrt{\dfrac{1-cosx}{2}}$

$=\sqrt{\dfrac{1-\sqrt{1-sin^2 x}}{2}}$

为进一步简化过程，我们可以构造一个迭代：

注意到上式满足 $S_n=\dfrac{n}{2}sin \dfrac{360 \degree}{n}$ ,其中$n$ 是6的倍数，

令$\dfrac{360 \degree}{n} =x$

则有 $sinx=\dfrac{2S_n}{n}$

$\Rightarrow sin{\dfrac{x}{2}}= \sqrt{\dfrac{1-\sqrt{1-(\dfrac{2S_n}{n})^2}}{2}}$

$\therefore S_{2n}=nsin \dfrac{x}{2}$

$=\sqrt{\dfrac{n^2-n\sqrt{n^2 - 4 S_{n}^2}}{2}}$

由此我们可通过 $S_{24}$ 通过这种迭代算出 $S_{48}$

计算结果为 $S_{48} \approx 3.132$ ，同理，$S_{92} \approx 3.139$ ，$S_{1472} \approx 4.141583$

想看更多的吗？

$S_{5888} \approx 3.14159206$ ，

$S_{11776} \approx 3.14159262$ ，

$S_{94208} \approx 3.1415926513$ ，

可见尽管我算到了圆内接正94208边形的面积，也仅能精确到小数点后8位。

实际上，古人的计算能力不可与现代电脑相比，如刘徽尽毕生之力也仅算到了正3072边形，精确到了小数点后4位，但这仍是当时世界上最精确的数值。在南北朝时期，祖冲之在刘徽这一基础上继续努力，将圆周率精确到了小数点后7位，这意味着他至少要算到正11776边形的面积。在西方，这一成绩是韦达于1593年取得的，比之祖冲之晚了一千一百多年。