平面直角坐标系

平面直角坐标系

数轴

下图是一条数轴，数轴上的点与实数是一一对应的. 数轴上每个点都对应一个实数，这个实数叫做这个点在数轴上的坐标.

例如，点A在数轴上的坐标为-4，点B在数轴上的坐标为2. 反过来，知道数轴上一个点的坐标，这个点在数轴上的位置也就确定了. 例如，数轴上坐标为5的点是点C.

数轴可以确定直线上点的位置，但不能确定平面上点的位置，在平面上，需要两个坐标来确定点的位置.

平面直角坐标系

如下图，在平面内画两条互相垂直、原点为重合的数轴，组成平面直角坐标系（rectangular coordinate system）. 水平的数轴称为 $x$ 轴（x-axis）或横轴，习惯上取向右为正方向；竖直的数轴称为 $y$ 轴（y-axis）或纵轴，取向上方向为正方向；两坐标轴的交点称为平面直角坐标系的原点.

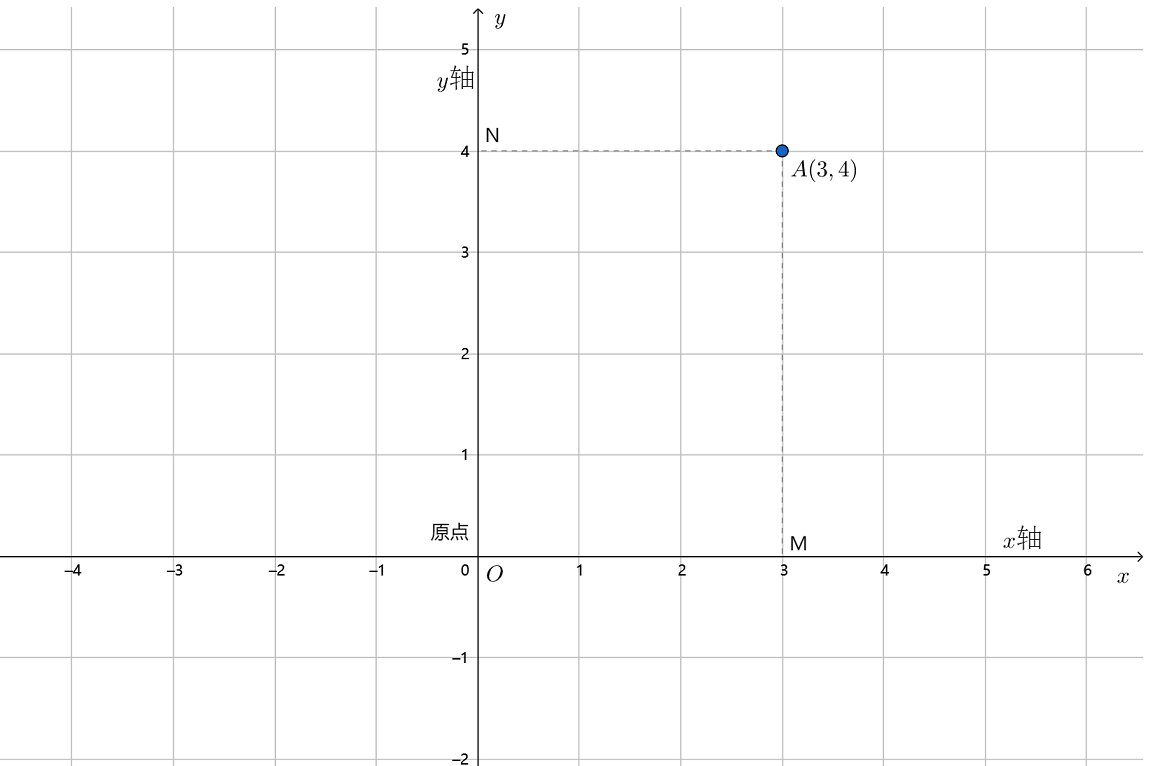
有了平面直角坐标系，平面内的点就可以用一个有序数对来表示了. 例如上图中由点A分别向 $x$ 轴和 $y$ 轴作垂线，垂足M在 $x$ 轴上的坐标是3，垂足N在 $y$ 轴上的坐标是4，我们说点A的横坐标是3，纵坐标是4，有序数对（3，4）就叫做点A的坐标（coordinate），记作A(3,4).

可以看出，原点O的坐标为（0，0）；$x$ 轴上的点的纵坐标为0；$y$ 轴上的点的横坐标为0.

建立了平面直角坐标系以后，坐标平面就被两条坐标轴分成四个部分，每个部分称为象限（quadrant），分别叫做第一象限、第二象限、第三象限、第四象限，如下图. 坐标轴上的点不属于任何象限.

笛卡儿

笛卡儿，最早引入坐标系，用代数方法研究几何图形

勒内·笛卡尔（又译作热奈·笛卡尔），1596年3月31日生于法国安德尔-卢瓦尔省的图赖讷（现笛卡尔，因笛卡尔得名），1650年2月11日逝世于瑞典斯德哥尔摩，是世界著名的法国哲学家、数学家、物理学家。他对现代数学的发展做出了重要的贡献，因将几何坐标体系公式化而被认为是解析几何之父。他还是西方现代哲学思想的奠基人，是近代唯物论的开拓者且提出了“普遍怀疑”的主张。黑格尔称他为“现代哲学之父”。他的哲学思想深深影响了之后的几代欧洲人，开拓了所谓“欧陆理性主义”哲学。堪称17世纪的欧洲哲学界和科学界最有影响的巨匠之一，被誉为“近代科学的始祖”。