青羽讲数学史（二）

青羽讲数学史（二）

数学长征，青羽

关于黄金比例，在数学、自然、人文中都有诸多体现。数学中，例如黄金矩形、黄金三角形、黄金椭圆、黄金双曲线等，其中比较有趣的是斐波拉契数列。

13世纪意大利数学家斐波拉契在他的《算盘经》中提出了一道著名的兔子繁殖问题，为黄金分割大放异彩。问题是：一对兔子每一个月可以生一对小兔，那么，从刚出生的一对小兔算起，满一年可以繁殖多少对兔子？

则由第一个月到第十二个月兔子的对数分别是：1,1,2,3,5,8,13,21,34,55,89,144，这个数列称为斐波拉契数列。它的特点在于，从第三项起，每一项等于它的前两项之和，即F(n)=F(n-1)+F(n-2),(n≥3)

与其简单的形式不相符的是通项公式的复杂程度：

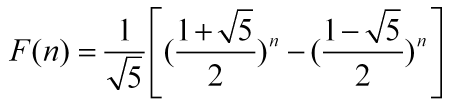
奇妙的是公式中含有无理数根号5,而n用正整数代入时，所得的结果却都是正整数；另一出人意料的是，相邻两项的比Fn/F(n+1)，当n趋于无穷大时，它的极限恰好是黄金比例.

斐波拉契数列具有特殊、神秘的魅力，难怪前些年国外出版了一种《斐波拉契数列》杂志，专门发表有关这个数列的新发现和新用途的文章，使得斐波拉契数列的研究长盛不衰，生生不息。

在自然界，树的一枝上各叶片按螺旋形上升的距离刚好按黄金比排列，因为这种排列叶片的受光效果更好。从而可启发建筑师设计出使房间接受阳光最充足的新颖高楼大厦。此外，人体中也存在黄金比例。我想今年高考全国一卷的考生应该对它的印象尤为深刻:

这神奇的黄金比例为什么能使得艺术家和数学家都对他情有独钟呢？其魅力究竟何在呢？古希腊哲学家、数学家柏拉图说：“美就是恰当。”法国数学家、哲学家笛卡尔说：“美是一种恰到好处的协调和适中。”先哲们的说法，也许就是恰当的解释。

三、毕达哥拉斯——最早的学霸

“学霸”这个词，现在就是指学习特别好的人。但是学霸这个词的本意并非如此，而是指那些在学术界利用自己的地位铲除异己，打压其他人的坏蛋，也叫“学术界的恶棍”。

前面说到，毕达哥拉斯学派的观点是“万物皆数”，而且都是整数（或者整数的比），他们认为宇宙的本质就是数，研究数学就是研究宇宙。

毕达哥拉斯学派发现了毕达哥拉斯定理（勾股定理），即一个直角三角形的两条直角边的平方和等于其斜边的平方。并且证明了无论是整数、有限小数还是无限循环小数，都可以写作一个分数的形式，其分子分母都为整数。

在毕达哥拉斯学派为自己的丰硕成果沾沾自喜时，有一天，学派内部一个年轻学者希帕索斯提出了一个疑问。

 “如果一个直角三角形的两个直角边都是1，那么斜边的长度如何表示成两个整数的比呢？”显而易见，根据勾股定理，斜边的长度是根号2。但是根号2如何才能表示成两个整数的比呢？希帕索斯为这个问题苦苦思索却没有答案，他只好求助于他的老师——毕达哥拉斯。

天真的希帕索斯以为毕达哥拉斯会给他答案，可谁知道，希帕索斯的问题居然动摇了毕达哥拉斯学派信仰的基础——万物皆数。毕达哥拉斯实在无法解答这个问题，但是他又不想推翻自己已经建立的对数和宇宙的信仰。

最终，毕达哥拉斯选择隐藏这个问题，他把可怜的希帕索斯扔进了爱琴海里去淹死了。希帕索斯受尽了同门的唾骂，成为历史上为探究真理而献身的人，而毕达哥拉斯则成为历史上第一位学术界的恶棍——学霸。

四、风波未平

前面说到，毕达哥拉斯学派对“形数”的研究尤为推崇，而正方形是几何学中最简单的图形之一，受收到教徒们的尊崇也是自然而然的。（正方形有4条边，分别对应四大元素，即地、风、水、火。毕达哥拉斯认为，因为有了数，才有几何学上的点，有了点才有线面和立体，有了立体才有这四种元素，从而构成万物，因此正方形象征着数字的完美和谐）

然而，正方形的纯粹中却掺杂着无理数的魅影。若在正方形里画上一条对角线，无理数旋即浮出水面，即和希帕索斯提出的疑问一样。

希帕索斯提出的疑问是对毕达哥拉斯学派的一大冲击。倘若简单如正方形都能够使比例关系这一神圣语言手忙脚乱，它又怎么可能有能力掌控自然万物呢？毕达哥拉斯学派难以接受这一点，但它又是那样不容置疑，因为这是在他们奉行的数学规则下推导的结果。

毕达哥拉斯学派很快又发现，被他们奉为美与理性的终极象征的黄金比例，竟然也是一个无理数！真可谓雪上加霜。为了不让这些可怖的数字将毕达哥拉斯学派的教义信条毁灭殆尽，他们严守无理数的秘密，每一个人都守口如瓶，甚至连记录笔记也不被允许。不可通约的根号2由此成为毕达哥拉斯学派中埋藏最深也最为沉重的秘密。

但是，纸是包不住火的。无理数的出现动摇了毕达哥拉斯学派乃至古希腊哲学体系的根基，最终古希腊数学家们经过百年来的思想斗争，才平息了这场浩劫。整个这次事件被后世称为——“第一次数学危机”.