圆锥体积公式推导过程1

设圆锥体的高为$h$ ，底面半径为 $r$ ，

把圆锥切分为 $k$ 份，下图分别为从侧面看和从顶向下看

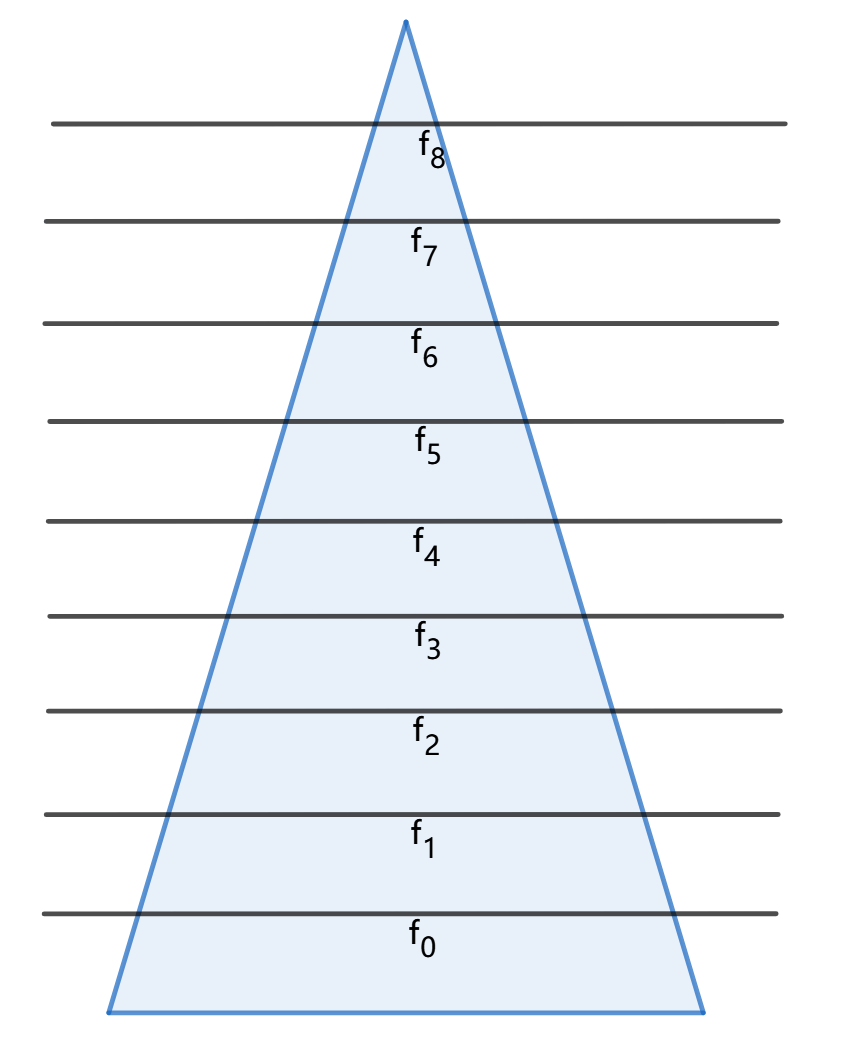
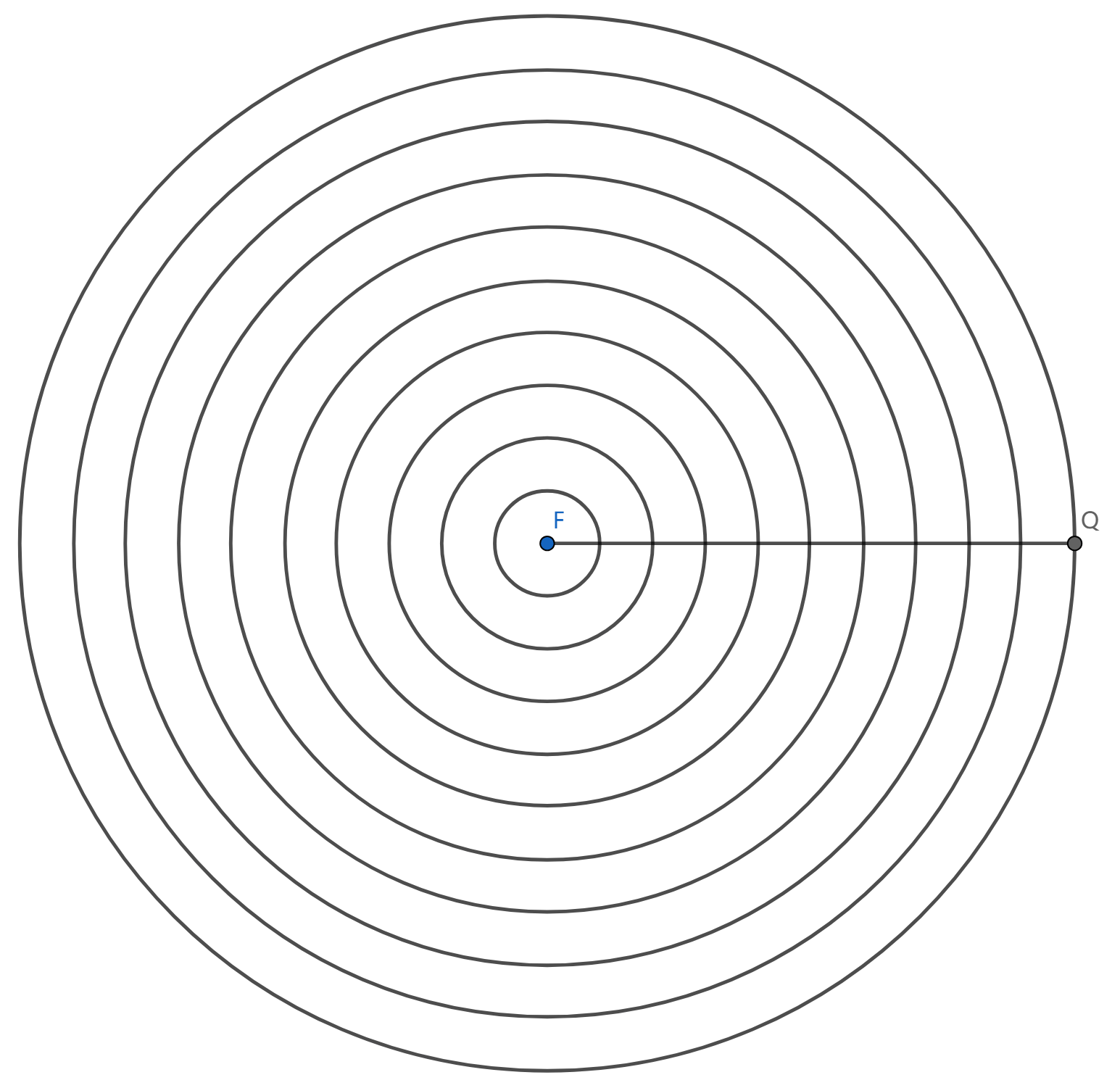
则每一份的高为 $\dfrac{h}{k}$ ，

从顶向下，第$n$ 份的底面半径为$\dfrac{nr}{k}$ ，

从顶向下，第$n$ 份的底面面积为$\pi(\dfrac{nr}{k})^2$ ，即$\dfrac{\pi n^2 r^2}{k^2}$

当切分数很多时，每一份可以看成一个圆柱体，于是

从顶向下，第$n$ 份的体积为$\dfrac{\pi h n^2 r^2}{k^3}$ ，

于是总体积为（将$n$ 替换为1到$k$ ,求和）：

$V=\dfrac{\pi h r^2(1^2+2^2+3^2+4^2+\cdots+k^2)}{k^3}$

在第248题中我们得到自然数的平方和经验公式：

$1^2+2^2+3^2+4^2+\cdots+k^2=\dfrac{k(k+1)(2k+1)}{6}$

代入总体积公式，得到

$V=\dfrac{\pi h r^2 k (k+1) (2k+1)}{6k^3}$

上式中的右则，再写详细一些

$V=\dfrac{\pi h r^2}{6} \centerdot \dfrac{k}{k} \centerdot \dfrac{k+1}{k} \centerdot \dfrac{2k+1}{k}$

所以有

$V=\dfrac{\pi h r^2 (1+\dfrac{1}{k}) (2+\dfrac{1}{k})}{6}$

当切分数很多很多时，$k$ 趋近于无穷大，所以$\dfrac{1}{k}\approx0$

于是得到

$V=\dfrac{1}{3} \pi r ^2 h$