托勒密定理及其推论

托勒密定理及其推论

托勒密

亚历山大的托勒密（Claudius Ptolemy）生活于大约公元2世纪。一般几何教科书中的“托勒密定理”，实出自依巴谷(Hipparchus)之手，托勒密只是从他的书中摘出.

托勒密定理

圆内接凸四边形两对对边乘积的和等于两条对角线的乘积.

如图， $BC \times AD + CD \times AB$ $=AC \times BD$

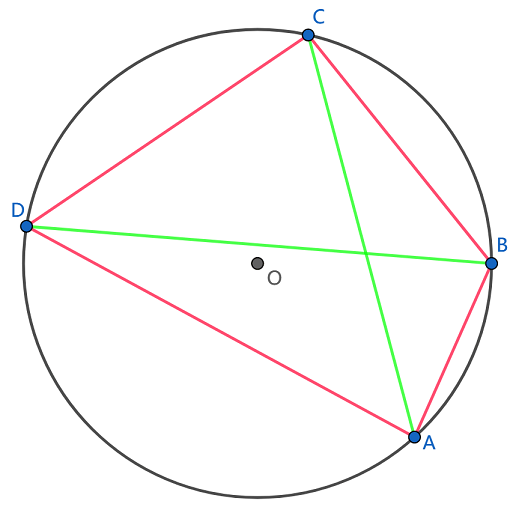
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式，托勒密定理实质上是关于共圆性的基本性质．

对比

在一条线段AD上，顺次标有B、C两点，则AD·BC+AB·CD=AC·BD (欧拉).

证明

（1）如下图所示。

不妨设∠ACB大于∠ACD。于是，在∠ACB内作一个以点C为顶点、以CB为一边的∠BCE，使∠BCE=∠ACD（图(1)中的红色角）。又由于∠CAD=∠CBE（同弧同侧的圆周角相等），所以三角形ACD与BCE相似. 于是有AD : BE = AC : BC，即AD·BC=AC·BE（称为1式）.

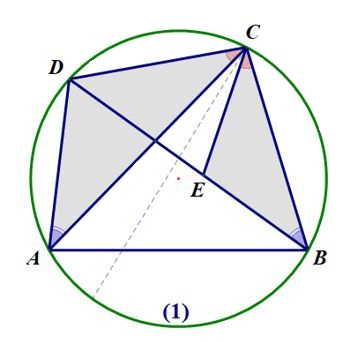
（2）同理，如下图图(2)所示，三角形CDE与ABC相似。从而有CD : AC = DE : AB，即AB·CD=AC·DE（称为2式）.

（3）1式加上2式，即得AD·BC+AB·CD=AC·(BE+DE)=AC·BD. 即

AC·BD=AB·CD+AD·BC

证毕。

几个推论

（1）点P位于等边三角形ABC外接圆的劣弧AB上，则有PC=PA+PB.

证明：如下图所示，由托勒密定理，在四边形APBC中，PC·AB=PA·BC+CA·PB.

而等边三角形三边相等，即AB=BC=CA，所以，PC=PA+PB.

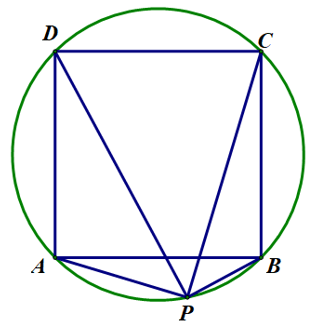
（2）点P位于正方形ABCD外接圆的劣弧AB上，则有(PA+PC)PC=(PB+PD)PD.

证明：如下图所示，由托勒密定理，在四边形APCD中，PD·AC=PA·DC+PC·AD；在四边形BPDC中，PC·BD=PB·DC+PD·BC；因为正方形四边相等，我们设它为a.

于是，上两式成为：PD·AC=PA·a+PC·a (1式)；PC·BD=PB·a+PD·a (2式).

1式乘以PC，2式乘以PD，得PC·PD·AC=(PA·a+PC·a)·PC (3式)；PD·PC·BD=(PB·a+PD·a)·PD (4式).

因为正方形对角线AC=BD，所以，3式和4式的左侧是相等的，于是，3式和4式的右侧也相等。所以有(PA·a+PC·a)·PC = (PB·a+PD·a)·PD.

两边约去a，得(PA+PC)·PC = (PB+PD)·PD.

（3）对正五边形和正六边形，应用托勒密定理，可以得到类似的结论。我只给出结论，证明自己试一试.

如图，点P位于正五边形ABCDE外接圆的劣弧AB上，则有PC+PE=PA+PB+PD.

点P位于正六边形ABCDEF外接圆的劣弧AB上，则有PD+PE=PA+PB+PC+PF.

（4）托勒密不等式

凸四边形的两组对边乘积和不小于其对角线的乘积，取等号当且仅当共圆或共线.

任意凸四边形ABCD，必有AC·BD≤AB·CD+AD·BC，当且仅当ABCD四点共圆时取等号.