海伦公式的简洁式

海伦公式

海伦公式又称为海伦－秦九韶公式。它是利用三角形的三条边的边长直接求三角形面积的公式。表达式为：

$S=$ $\sqrt{p(p-l_a)(p-l_b)(p-l_c)}$

其中$S$为三角形的面积中$l_a$ ，$l_b$ ，$l_c$分别为三角形三边长，$p$ 为半周长.

它的特点是形式漂亮，便于记忆。 相传这个公式最早是由古希腊数学家阿基米德得出的，而因为这个公式最早出现在海伦的著作《测地术》中，所以被称为海伦公式。中国秦九韶也得出了类似的公式，称三斜求积术。

请注意以下内容

三角形不同的面积公式对应不同的分割方法。$S=\dfrac{1}{2}hb$ ，二分之底乘高对应的是割补矩形法，而海伦公式对应如下的内切圆分割法：

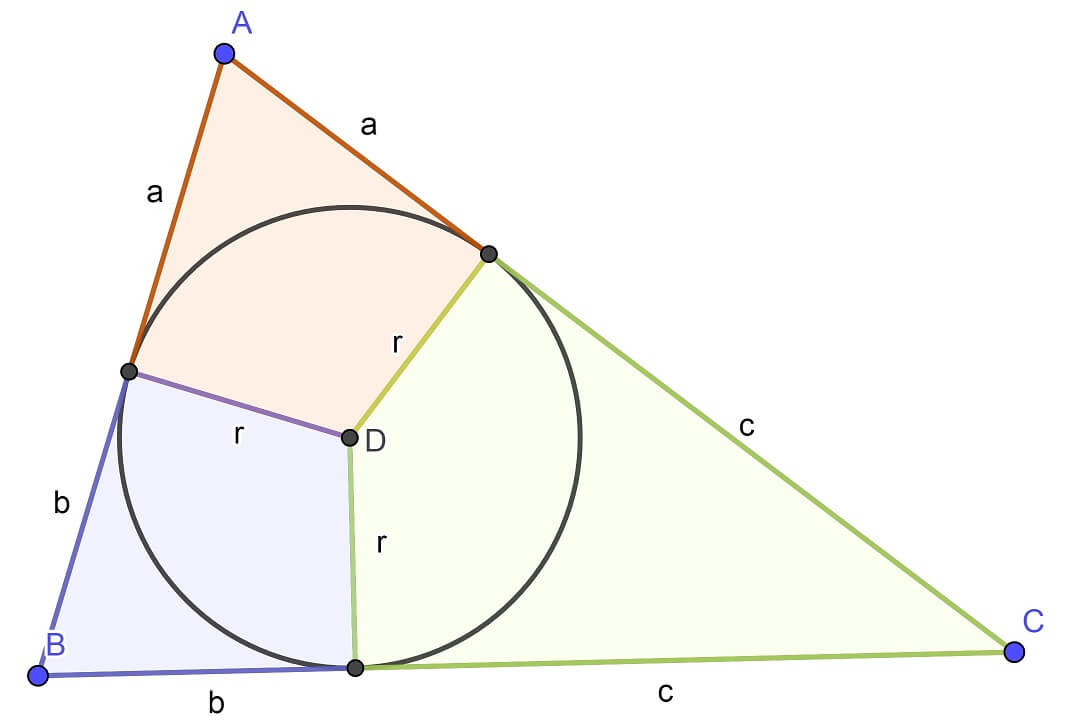
此时面积公式为

$S=(a+b+c)r=pr$

其中p就是半周长，而内切圆半径r满足

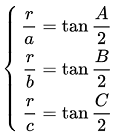
将$C=\pi-A-B$ 代入后，利用$\tan$ 的和公式就可以得到

$r^2=\dfrac{abc}{a+b+c}$

即

$S=\sqrt{(a+b+c)abc}$

$=\sqrt{p \cdot abc}$

这应该就是海伦公式最简明的样子，是否极其舒畅？最后，将$a$ 、$b$ 、$c$ 用边长重新表达，即，记$l_a$ 、$l_b$ 、$l_c$ 为边长，有

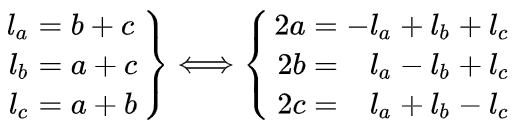
至此，海伦公式变成了大家所熟知的样子，没有刚才舒畅了.

$S=\sqrt{p(p-l_a)(p-l_b)(p-l_c)}$