抛物线的焦点弦的性质

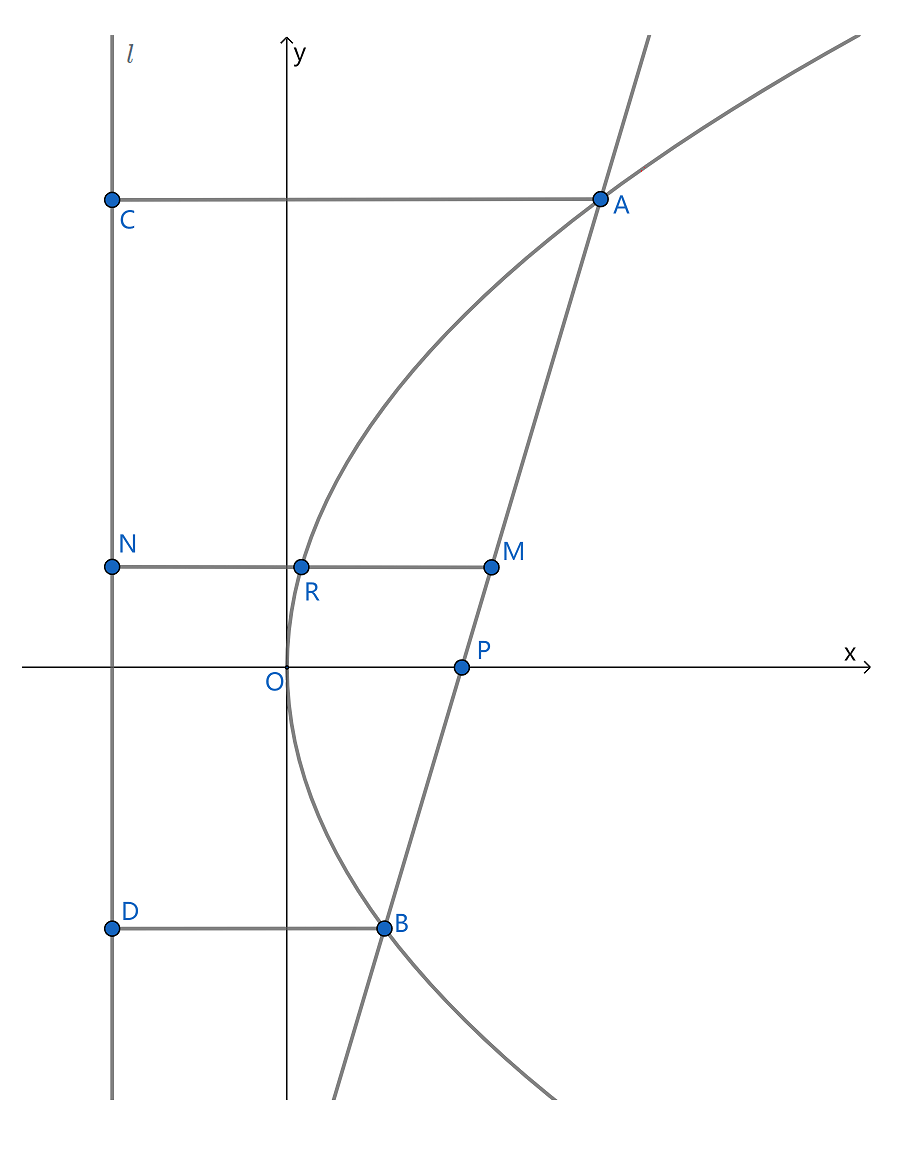
上图中, $AB$ 是过抛物线 $y^2=2px$ $(p>0)$ 的焦点的弦, 称为焦点弦, 其中 $F$ 是焦点, 直线 $l$ 是其准线, $A$ 点坐标$(x_a,y_a)$ , $B$ 点坐标 $(x_b,y_b)$ , $AC \perp l$ , $BD \perp l$ , 且 $M,N$ 分别是 $AB,CD$ 的中点, 抛物线的焦点弦有以下性质:

A. $y_a y_b =-p^2$ , 且 $x_a x_b =\dfrac{p^2}{4}$

B. $\angle CFD =90 \degree$ , 且 $NF \perp AB$ , $AN \perp BN$

C. $|AB|=x_a +x_b+p$

D. $|AB|=\dfrac{|y_a-y_b|^2}{2p}$

E. $|AB|=\dfrac{2p}{\sin^2 \theta }$ ($\theta$ 为 $AB$ 的倾斜角)

F. 直角梯形 $ABCD$ 的对角线交于原点$O$ , 且 $S_{\triangle AOB}=S_{\triangle COD}$ =$\dfrac{p}{4}|y_a -y_b|$

G. $MN$ 被抛物线平分, 交点 $R$ 为 $MN$ 的中点

H. $|RF|=\dfrac{1}{2}|MN|$ $=\dfrac{1}{4}AB$

I. $\dfrac{1}{|AF|}+\dfrac{1}{|BF|} =\dfrac{2}{p}$

J. 以 $AB$ 为直径的圆和准线l相切