数理估算

数理估算

z张z

数学往往要求较为严谨，但在现实生活中也有很多情况我们没办法得到如计算中那样准确的数据，比如某施工单位测量弧垂的高度，事实上这些人知道差不多就可以(甚至偏差2-3厘米)，再者很多人在金钱数目上的花销做估算，这点我深有体会，我总是错误的估算买买买导致月底不得不承担一些后果，笔者曾在数学建模中给出的答案完全是通过估算得来的。换句话说，我们每天有相当多的时间用来估算，说的好听些不妨称这些估算为 “生活中的数学模型” 。

生活中应用估算的例子有很多，一个简单的例子是计算(手机)流量，众所周知1G=1024M，我敢打赌的说绝大部分人估算自己用的流量都是按照1G $\approx$ 1000M来算的。再如问哈尔滨有多少加油站ⁱ——这种面试中的奇怪问题——也叫做费米问题。这些数值的估算往往来自于生活经验，如果逐一列出，我想恐怕怎么也说不完，所以，不妨来看看数理中那些神奇的估算技巧。值得注意的是，这里估算的意思更多的是指预计、估计，或者是误差在允许的范围内所给出的答案。

牛顿二项式定理ⁱⁱ

当 $x$ 远小于1时，有

$(1+x)^{n} \approx 1+nx$

为什么要远小于1？我们在做估算时有一个度，比如0.01与10000相比完全可以舍去，与0.05、0.1相比则完全不能忽视，这个公式里出现了1，当然要与1相比较，或许可能很多人都了解这个公式，但没怎么用过，这大多是因为考试不允许这样做。然而这确实是一个实用的公式。

如我们熟知的相对论动能

$E=mc^{2}$

实际上这是一个通俗的写法，标准应写成

$E=\gamma mc^{2}-mc^{2}$

其中

$\gamma \equiv (1-\frac{u^{2}}{c^{2}})^{-\frac{1}{2}}$

这里的 $u/c$ 就满足远小于1的情况(平方就更加满足)，所以我们通常将E做

$E=mc^{2}[(1-\frac{u^{2}}{c^{2}})^{-\frac{1}{2}}-1]$

$\approx mc^{2}[1+\frac{u^{2}}{2c^{2}}-1]$

$=\dfrac{1}{2}mu^{2}$

这是每个高中生必学的动能公式。

概率估算

不知道大家对熵有无了解，它是热力学中的物理量，代表物质混乱的程度，通常用S表示，熵只增不减，一切总是朝着愈加混乱状态的进行。在不同的领域有着不同的表达式，如在统计热力学中

$S=k \log \Omega$

其中 k 是常数，Ω 是微观状态粒子数。在信息领域则为

$S=-\sum_{x} p \log(p)$

其中 x 是事件，p 是事件概率。我们重点讲述后者，很多概率可以用它解释比方我们掷一枚硬币，它只能是正反面中的一种情况，这样我们可以得到公式：

$S=-p \log(p)-(1-p) \log(1-p)$

S最大时p为0.5，于是我们认为抛硬币正反概率为0.5，抛开这些公式我们会认为0.5是很正常的现象，这是因为抛硬币太常见了，我们有了生活经验，而如果是纯理论的抽象问题ⁱⁱⁱ，我想还是老老实实的套公式吧！但不能认为我在一次考试中满分与非满分的概率也为0.5，我不知道硬币的其它信息(不知道这枚硬币有没有做过手脚)，而我却知道自己了解的信息远小于试卷上包含的信息。

有了以上知识，我们可以在了解了信息的基础上使得熵最大据此来估计某些概率，如针对某事件我们知道

$\sum_{x}px=k$

那么这个额外信息配合

$S=-\sum_{x}p \log(p)$

得到的函数关系就能估计出事件的概率，完全根据我们掌握信息的多少。

积分估算

多元函数微积分教材上对估算的内容介绍的不多，但会有这样的计算题：估算$2.20^{1.98}$ ，用二元微分不难计算，设$f(x,y)=x^{y}$ 全微分后代入上式的各值，就再无多少关于估值的介绍了，或许是与计算机软件配合密切，因为计算量偏多。考虑到实用性，我简要提一下插值估算方法，这部分内容不是很主要，读者可以在阅读时略去这部分或仅做了解。

首先微积分初学者会了解到

$\int^{b}_{a}f(x)dx$ $\approx \sum_{i}\Delta x_{i}f(x_{i})$

也就是切割很多矩形的面积和，但实际上有一种误差更小的方法，不用矩形而是用梯形。

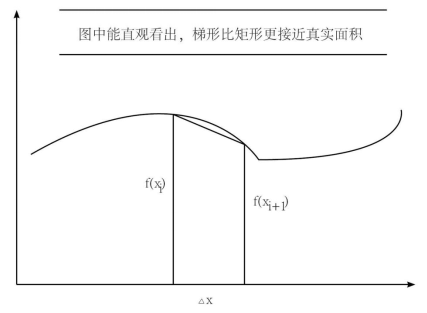
这样新的替代公式^iv

$\int^{b}_{a}f(x)dx\approx$ $\sum_{i}\frac{f(x_{i})+f(x_{i+1})}{2}\Delta x$

无一例外都是插值方法，在此基础上慢慢发展出数值分析法：牛顿-科斯特公式与辛普森法则，我们来看辛普森法则，该方法主要是通过分区间后用二次曲线逼近得到微积分近似解，当然，大多是没有原函数的积分，如下：

$\int^{b}_{a}f(x)dx\approx$ $\frac{b-a}{6}[f(a)-4f(\frac{a-b}{2})+f(b)]$

a，b间隔越小，结果就越精确，推导过程是根据拟柱体^v 推导的，根据拟柱体不同有不同的推导版本。

微分方程估算

微积分估算的例子很多，如线性近似:

$f(x)\approx$ $f(x_{0})+f^{\prime}(x_{0})(x-x_{0})$

微分方程，尤其是高阶微分方程确实不太好算，教材上的题大多是被编造好有特定的简便的计算方法或是技巧，实际生活却不是这样，但实际生活中一个好处，我们往往拥有多组解的数据，比方说求水温随时间，气压的变化率，这就是一个微分方程，而大量数据只要烧一壶水就得到了，这些数据就成了我们作为估算的依据。来看一个历史上著名的例子，天体的轨道运行，为了方便讲述我们先抛开背景只关心其中的技巧，我们以一个微分方程为例:

$\frac{d^{2}y}{dx^{2}}+y=k$

这是个二阶微分方程也不难解，它的解是

$y=c_1 \cos x+c_2 \sin x+k$

其中c1，c2，k是常数，方程大概是说行星绕日的轨迹是椭圆，随后这个方程被认为不够精确，被改写成新的形式：

$\frac{d^{2}y}{dx^{2}}+y$ $=k_{1}+k_{2}y^{2}$

这样一来可给方程增加了不少难度，当然就用到估算方法了，这个新方程是第一个方程的精确形式，那么不妨将第一个方程的解当做这个新方程的一阶近似($y_{1}$ )，将一阶近似代入方程得到的解当做二阶近似($y_{2}$ )，如此往复或者选择忽略高阶项，这样我们就得到一个二阶近似解。也就是：

$\frac{d^{2}y_{2}}{dx^{2}}+y_{2}\approx$ $k_{1}+k_{2}y^{2}_{1}=$ $k_{1}+k_{2}(c_{1} \cos x+c_{2} \sin x+k)$

这样通过计算后得到

$y_{2}\approx$ $y_{1}+k_{2}k^{2}[1$ $+k\sqrt{c^{2}_{1}+c^{2}_{2}}+x \sin x$ $+k^{2}_{2}k^{4}$ $[\dfrac{1}{2}-$ $\dfrac{1}{6} \cos(2x-x_{0})]]$

其中除 x 外皆为常数，如此一来，我们得到一个微分方程的近似解，它与标准解的误差不过千分之一，在实际的数理计算中非常实用。

总结

笔者从几个角度浅谈了估算的用处，虽然侧重在数学物理方面，然而也有很多不熟悉的领域方面没有具体展开，如计算机博弈论，人机如何自我学习击败用户，这些涉及到估值函数，局面分析，往往需要引入权值或是衰减因子方可正确落子。再者估值活跃与造价估算，谐波估算，储量估算等无数其它方面，这些与数学有很强的交互作用。希望读者多多留意身边事物，知微见著，知小见大，以直代曲，以虚求实！

最后来看一个饶有趣味的估值问题“斐波那契数列与贝祖数的估计”，不久前谈方琳这位女初中生因发现了贝祖数组斐波那契数列的联系被媒体大为赞赏，蝉联“最年轻科学家”那么她研究的贝祖数是什么呢？它来源于一个问题px+qy=r，如果p,q,r都是整数，那么x,y有没有整数解？随后被数学家克劳德-加斯帕·巴歇·德·梅齐里亚克给出充要条件(也就是贝祖定理)，裴蜀因为对本问题的研究贡献巨大，贝祖定理又叫做裴蜀定理，如下:

若p,q是整数,且gcd(p,q)=r (r是p和q的最大公因数/公约数)，那么对于任意的整数x,y,px+qy都一定是r的倍数，特别地，一定存在整数x,y，使px+qy=r成立。

比如12是24和60的最大公约数，那么 $24x+60y=12$ 一定有整数解，我们可以用辗转相除法求得它的解。当然解并不是唯一的，可以有多组解或者无穷解，那么解的范围有多大呢，也就是确界问题，这个确界也就是谈方琳所研究的课题，具体如图所示，不过多赘述。随后数学爱好者们从不同角度出发又相继给出了多种等同的估值方法，有兴趣的读者可以查询相关资料获取。

i 显然你的面试官只是想考考你的逻辑，但它的确需要一些生活经验，我们不妨按照逻辑估算一下。第一种方法：如果我想要打车去往某一目的地，有些时候司机或许会询问我们能否等几分钟来加油，这通常耽误不了多长时间，我们假设有一辆车需要加油，他在五分钟左右就能寻找到一个加油站，那么据此估算加油站的数目约等于哈尔滨占地面积除这位司机五分钟能够行走的面积，哈尔滨国土面积大约是5.3万平方公里，再假设汽车平均时速50千米每时，五分钟内他行走的面积是距起点为圆心的圆，π取3，则哈尔滨加油站总数

$=\dfrac{53000}{3\times (\dfrac{50}{12})^{2}}$$\approx 1018$ 。

第二种方法：哈尔滨约有200万辆车，假设每天只有60%的车会被使用，再假设这60%中只有5%需要加油，再假设这5%中只有1%的车辆在离我最近的某个加油站加油，那么加油站总数

$\approx 2000000\times 60\%\times 5\% \times 1\%$ $=600$

可以看见不同的方法差距是显见的，实际上还有多种方法，但数量级一定一致，估算大的数目尤为明显。

ii 这里指常用来做估算的

$(1+x)^{n}\approx1+nx$

实质上这是对前者的泰勒展开，然后忽略掉二阶以上的项，展开如下：

$1+nx+\frac{1}{2}n(n-1)x^{2}$ $+\frac{1}{6}n(n-1)(n-2)x^{3}$ $+o(x_{4})$

很多极限题目也这样做。

iii 概率之和真的是一吗？答案是肯定的，但物理学家霍金曾经给出质疑，这与他研究的黑洞有关，如果将熵值很大的物体扔进黑洞，那么这个熵凭空消失了，同时摧毁了一个定律，概率和为1，霍金老爷子立场也很坚定，认为黑洞的确摧毁了这个定律，并以同样的风格，做下赌注，不久后，他承认自己输了，然而晚年他仍然在研究这个问题。

iv 实际上，这样的方法比前者精确一倍，证明从略。

v 顶点全部在两个平行平面内的多面体叫做拟柱体。