青羽谈数学思想

青羽谈数学思想

一、数学思想是什么？

“数学思想”是一个范围很广的词，它指对数学事实与理论经过概括后产生的本质认识，换句话说就是把具体的数学知识都忘掉之后的东西。某种程度上说，数学思想是掌握数学的精髓。

数学思想不同于数学灵感。数学上的许多著名的数学发现，都是来自于转瞬即逝的灵感发现，如笛卡尔引入直角坐标系，庞加莱发现富克斯函数的变换方法，哈密顿推广复数至四元数等等。数学灵感就像是模糊隐约的雾中之花，只可意会不可言传；数学思想则至少可观其轮廓，具有一定的“形”。数学思想是“积之在平日”，数学灵感则“得之于俄顷”。

数学思想也不同于数学方法。“数学思想”往往是观念的、全面的、普遍的、深刻的、一般的、内在的；而“数学方法”往往是操作的、局部的、特殊的、表象的、具体的、技巧的。数学思想常通过数学方法去体现；数学方法也常常反映了某种数学思想。

由此在本文我想通过由具体问题的具体分析来体现出一定数学思想，同时也会在重要的地方加以讲解。

二、我个人的数学思想

数学家将数学思想分为了几个大类：函数方程思想、数形结合思想、分类讨论思想、方程思想、整体思想、化归思想、隐含条件思想、类比思想、建模思想、归纳推理思想、极限思想。在高中三年的学习中，我对这些思想方法的掌握和运用都还算比较熟练。

先谈谈我的认知吧。我曾听过一个绝妙的比喻：假如我们现在遇到一个问题，有一口锅，一袋面，一盆水，要怎么煮面？后来我们找到了解决问题的方法，把水倒进锅里，再把锅里的水烧开，再把面丢进去煮熟就行了。那么这个问题也就解决了，可是我们又遇到了另一个问题，有一口装有水的锅，一袋面，一盆水，要怎么煮面？一般人肯定想的是，直接把锅里水烧开，再把面煮熟就行了。但数学家的想法比较奇特，他说把锅里的水倒掉就行了。因为这个问题和第一个问题的唯一区别就在于，原先的空锅变成了有水的锅，那么我把水倒掉，这个问题就回到了第一个问题，而第一个问题是已解决的，那么这个问题也就解决了。

这个比喻虽有不当之处，因为现实中肯定没人这么干。但在我看来它却体现了一种数学思想：以退求进，将未知问题化为已知问题。

我先出一道数列的题来表达这个思想，请看下题：

例1.

若{ $a_n$ }是一个等差数列，$S_n$ 是 $a_n$ 的前 $n$ 项和，且满足

$\dfrac{S_{n-1} +S_n +S_{n+1}}{n}$$=3+3n+\dfrac{2}{n}$ $(n \geqslant 2)$ ，求{ $a_n$ }的通项公式.

思路:

由给定条件联想到一个常用结论：如果{ $a_n$ }是公差为d的等差数列，那么{ $\dfrac{S_n}{n}$ }也是一个等差数列且公差为$\dfrac{d}{2}$ .

于是想到将左式变形，那么3个S如何处理呢？我们不妨退一步，将 $S_n$ 用 $a_n$ 表达出来.

左式$=\dfrac{3a_1 +3a_2 + \cdots + 3a_{n-1} +2a_n +a_{n+1}}{n}$ ，

这样容易观察出，可以利用 $a_{n-1}+a_{n+1}=2a_n$ 将 $a_{n+1}$ 化掉，则

左式$=\dfrac{3a_1 +3a_2 + \cdots + 2a_{n-1} +4a_n}{n}$ $=\dfrac{3S_n}{n}+\dfrac{a_n -a_{n-1}}{n}$ ，

这个式子足可谓美观，又可将其表示为

$\dfrac{3S_1}{1}+\dfrac{3d}{2} (n-1) +\dfrac{d}{n}$

所以有

$3S_1 -\dfrac{3d}{2} +\dfrac{3d}{2} n +\dfrac{d}{n}$ $= 3+3n+\dfrac{2}{n}$ ,

易得到

$d=2$ ，$S_1=a_1=2$

所以

$a_n=2n$

这个例题就体现了以退求进的好处，如果我们直接从 $S_{n-1}+S_n+S_{n+1}$ 到 $3S_n+a_n-a_{n-1}$ 是有一定的难度的，正是从"S"到 "a"这一步，才使得左式的结构清晰明了。同时对于已知结论的熟练掌控、相似结构的触类旁通也极为重要。

第二点，关于转化与化归往往需要做题的熟练度和对式子及数字的敏锐程度。

我们都知道如果有式子 $\dfrac{1}{a}+\dfrac{1}{b}=m$ （m为常数），要求a+b的最小值，只需妙用“1”的代换让两式相乘即可，即

$a+b=\dfrac{1}{m}(\dfrac{1}{a}+\dfrac{1}{b})(a+b)$

$=\dfrac{1}{m}(1+1+\dfrac{b}{a}+\dfrac{a}{b})$ ，

然后对$\dfrac{b}{a}+\dfrac{a}{b}$ 用均值不等式即可。

如果所求式子的形状并不是常规形状，那么转换出想要的式子往往需要技巧，比如下题。

例2.

已知 $\dfrac{2}{a}+\dfrac{1}{b}=1$ ，求$\dfrac{4}{a-2}+\dfrac{3}{b-1}$ 的最小值。

思路：

观察两式，a与2总是相关联，b与1总是相关联，于是可以从右式的2和1入手.

解：

因为

$\dfrac{4}{a-2}+\dfrac{3}{b-1}$

$=\dfrac{\dfrac{4}{a}}{1-\dfrac{2}{a}}+\dfrac{\dfrac{3}{b}}{1-\dfrac{1}{b}}$

$=\dfrac{\dfrac{4}{a}-\dfrac{4}{ab}+\dfrac{3}{b}-\dfrac{6}{ab}}{1-\dfrac{2}{a}-\dfrac{1}{b}+\dfrac{2}{ab}}$

$=\dfrac{\dfrac{4}{a}-\dfrac{4}{ab}+\dfrac{3}{b}-\dfrac{6}{ab}}{\dfrac{2}{ab}}$

$=\dfrac{3a+4b-10}{2}$

又

$3a+4b=(\dfrac{2}{a}+\dfrac{1}{b})(3a+4b)$

$=6+4+\dfrac{8b}{a}+\dfrac{3a}{b}$

$\geqslant 10+4\sqrt{6}$

代入，得

右式 $\geqslant \dfrac{10+4\sqrt{6} -10}{2}$ $=2 \sqrt{6}$

这道题的关键在于找到和总是变量相关联的数字，从此入手便可很快转化成我们想要的形式。不过所谓“横看成岭侧成峰，远近高低各不同。”意思是我们观察事物，如果所处的立场不同，观察到的结果也会不同。我们思考处理某一个数学题，如果从某一角度用某种方法解决难以奏效时，不妨换一个角度去观察，换一种方法去处理。

还是以这道题为例，如果没观察出关联的变量和数字，也可用利用条件中的“1”用三角函数的方法。设2/a＝cos²θ，1/b＝sin²θ，再将此关系代入式中，同样可以解决问题。

下面再举一道例题谈一下建模思想。

例3.

证明世界上任意6个人中，总存在3个人互相认识或互相不认识。

这是一道典型的拉姆齐理论问题，先给这6个人编号为ABCDEF，理论上我们可以枚举出所有的情况，最后推出结论。但这种方法太过繁琐，并且有些“暴力”。

如果能体现出建模思想，那么这问题也就迎刃而解了。把每个人看作一个点，两个人之间的关系用线段表示，由于两个人只可能存在两种关系：认识或不认识，可对线段进行涂色，不妨以红色表示认识，蓝色表示不认识。现在的问题简化到：任选6个点，并把每两点之间连线，并对每条线涂上一种颜色，那么是否必然存在一个同色的三角形？

通过这种建模我们做到了人物之间关系的可视化，那么这个问题现在看来就更具直观性.

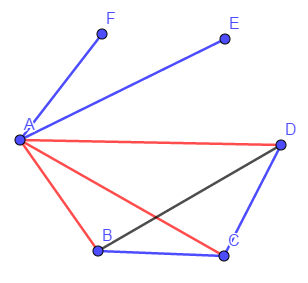
不妨先考虑A，在A与其它五点的五条连线中涂上红蓝两色，由鸽巢定理，至少存在三条线都为同一颜色。不妨设AB、AC、AD为红色，那么如果要避免产生同色三角形，BC、CD仅可涂上蓝色，可是这时BD无论涂什么颜色，都会出现同色三角形，因此同色三角形必然存在。

在这个模型中，问题已得到简化。再通过一次鸽巢定理，大大缩小了考察的范围，能使问题再次简化。由此可见数学思想的体现的往往不是单个思想，而是多种思想结合起来体现的。

下面再说一个故事，来谈一下极限思想以及对我新知识的理解方式。

我高二刚学导数的时候，老师说“一个点的导数就是这个点在图像上切线的斜率。”我对此不满，并认为应该说成是斜率的最佳近似值。因为高中对“极限”的讲述实在是太少了，以至于难以对导数及微积分做到真正本质上的理解。在我的理解中，当△x越来越小时，输出值与真实斜率之间的误差也越来越小，直至可忽略不计，因此称为最佳近似值，即无论你用什么刻度去衡量，都测不出它的误差。

我始终认为导数与“真实斜率”是存在误差的，只不过误差是一个大于0但测不出来的数。在当时我并没有接触到本质上的“极限”思想，但我能有这方面的理解，现在想来也足为可贵。事实上，我的疑问在第二次数学危机期间，正是数学家所不能理解的核心思想——极限。

让·勒朗·达朗贝尔说：“一个量要么等于0，要么不等于0.若等于0，它早已消失无痕；若不等于0，便不可随意消除。介于两者之间的中间状态只能存在于幻想之中。”

在现代对导数的定义和牛顿、莱布尼兹的方法不一样，不同在于现代方法不会用0做除数，而是用一个趋近于0的量，这个量在现在已有完全合乎逻辑的定义，在此我也不加赘述。值得一提的是，有一首诗的意境与无穷小量极为相似“孤帆远影碧空尽，唯见长江天际流。”那“孤帆”就是一个在“长江”这条数轴上的一个点，向那无穷远处航行，最终消失于水天一际之中，这便是极限。

还有一个曾深深困扰我的问题是无穷集合的势。

先举个例子，大圆上的点和小圆上的点哪个多？

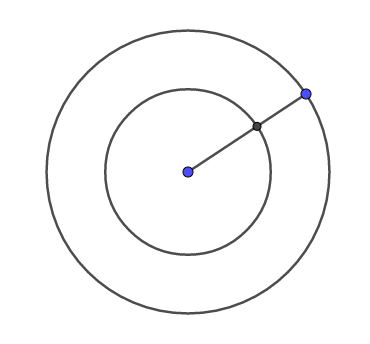
我们只需将两个圆的圆心放在一起，然后连接大圆上的半径，即可找出两个圆上的点存在一种一一对应关系，通过这种一一对应我们可知两圆上的点是一样多的。如果我们设集合A为所有大圆上的点构成的集合，集合B为所有小圆上的点构成的集合，那么可称集合A和集合B是等势的，即元素个数相同。 事实上如果存在着从集合A到集合B的一一对应关系，那么称A和B等势。

但有一天我发现一个事情：我可以建立从（0,1）上的全体有理数到（1，﹢∞）上的全体有理数的一一映射关系。我只需任取一个（0,1）上的有理数，然后作出它的倒数，便唯一对应了一个（1，﹢∞）上的有理数。那么（0,1）上的全体有理数到（1，﹢∞）上的全体有理数是否一样多呢？我曾一度怀疑我的结论的正确性，因为在（1，﹢∞）上有无穷多个（0,1）这样的集合，为什么两者还能等价呢？

数学有时候就是这么看似背乎逻辑，实则蕴藏真理。如果理解其背后的本质，这样的结果也不是不能接受。

事实上，任意两个区间上的有理数个数都相等。如果要验证这个命题的成立，只需构造一个对两个任意区间上的有理数的一一对应关系。关于它，我有一个绝妙的构造方式，但是限于本文篇幅不够，在这里我就不加赘述。

对于此类于生活常识相背离的事物，唯有以数学的眼光去看待，用数学思想去理解，才可以认识到它的合理性。

三、一些数学家的数学思想

3.1 欧拉——哥尼斯堡七桥问题

要提数学，不由得要提到大数学家欧拉（Euler）,13岁考入大学，16岁获硕士学位，一生发表书籍和论文高达886篇，据说彼得堡科学院为了整理他的著作，足足忙碌了47年。

欧拉一生的成就不胜枚举，其中有一项就是解决了哥尼斯堡七桥问题，这也成为图论、拓扑学的滥觞。哥尼斯堡曾是德国城市，后属苏联。普雷格尔河穿城而过，并绕流河中一座小岛而分成两支，河上建了7座桥。传说当地居民想设计一次散步，从某处出发，经过每座桥回到原地，中间不重复。

当地居民经过多次尝试都无果，他们不禁在想这种设计是否可行？于是他们把这个问题告诉了欧拉。欧拉拿到这个问题后，略一沉吟，便说“我可以将陆地简化为点，将桥简化为线，这样这个问题就等效于一笔画问题。”

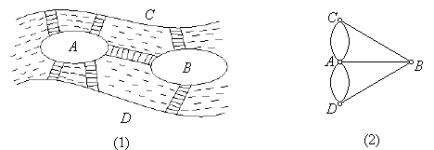
在欧拉这般精湛的数学眼光下，以上两图的几何性质的联通之处自然是无所遁形。我们只需在图2中，只用一笔画出这个图形，并且每条线只经过一次。然而即使简化成这样，欧拉也不能看出其是否能一笔画成。 欧拉认为，如果一些图形能够一笔画出来，那么这些图形必然满足某种条件。同理，若一些图形不能够一笔画出来，那么这些图形必然不满足某种条件。那么这种条件究竟是怎样的呢？答案应该就在图中最基本的元素——点。

点具有怎么样的性质？如果我们要用笔去画，必然有一个起点和一个终点。那么这里就有两个点比较特殊，若是起点和终点为同一点，那么就只有一个点比较特殊。

由这一个性质也不能得出什么条件，那么点是否还有其他性质呢？通过画了多个图形，欧拉发现有些点上面会有奇数条线，有些点上面有偶数条线。欧拉称这两类点为“奇点”和“偶点”。

如果一个点是起点，那么画的线必然有出无进，那线的个数应该是奇数，对于终点也是一样；而如果一个点是中间过程的点，那么画的线必然有进有出，那线的个数应该是偶数。需要注意的是，起点也可以作为中间过程的点，因为线画出后还可以再次经过起点，这样对起点增加了两条线，线的个数仍为奇数，对于终点也是一样。

欧拉由此得出结论：如果一个图形上，它仅有两个奇点或者0个奇点，那么它必然可以一笔画出。方法就在把奇点作为起点和终点，然后将其他的点依次连接即可。于是再观这个七桥问题，在图2中可见四个点都是奇点，那么它必然不可一笔画出。

这个七桥问题总算是解决了，可一笔画问题到了如今仍在继续。如果一个图中它有2n个奇点，那么画出这个图最少需要几笔呢？存不存在这样一个图，它里面有奇数个奇点呢？这两个问题留待读者自己思考。

3.2 罗巴切夫斯基与欧式几何第五公设

公元前三世纪，欧几里得集前人几何研究之大成，编写了数学发展史上具有极其深远影响的巨著《几何原本》。它以公理法建立了科学理论体系，并在开头提出了五个公设，其中前四个非常容易理解，但第五公设却富有争议，其内容可论述为过直线外一点，有且仅有一条平行线，因此它又叫做平行公设。

自公元前3世纪至19世纪初的两千余年中，数学家们投入了无穷无尽的精力试图由前四个公设推出平行公设，但他们几乎尝试了各种可能的方法，却都遭到了失败。

罗巴切夫斯基一开始也是循着前人的思路，但很快便意识到这些方法行不通。于是他另辟蹊径，大胆思索问题的相反提法：可能根本就不存在平行公设的证明。他的逻辑方法是，为证“平行公设不可证”，首先对平行公设加以否定，他假设过直线外一点，可以做两条平行线，然后用这个否定命题和其他公设组成新的公理系统，并由此展开推演。

首先假设平行公设是可证的，即平行公设可由其他公设推演出来，那么在新的公理系统中，必然会出现矛盾。

可是在推演过程中，罗巴切夫斯基得到了一连串古怪、不合常理的命题。但是经过反复审查，却没有发现它们之间存在任何逻辑矛盾。于是，远见卓识的罗巴切夫斯基大胆断言，这个新公理系统可构成一种新的几何，它的逻辑完整性和严密性可以和欧几里得几何相媲美。这种新几何后来被称为罗氏几何。

罗巴切夫斯基巧妙的反证法也是一种数学思想的体现。

3.丹迪林双球

这个仅在高中教材中占有不足2平方分米纸张的证明，确是我最喜欢的证明之一。

关于椭圆，它的定义为：平面内与两定点 F1、F2 的距离的和等于常数 2a （2a＞|F1F2|）的动点P的轨迹叫做椭圆。

但作为圆锥曲线的一种，椭圆还可由平面去切圆锥得到。

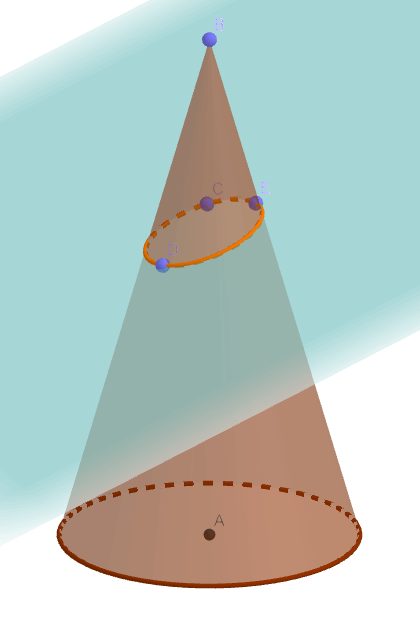
图中的相交曲线即为椭圆。那么这两种定义是否等价？丹迪林有一个绝妙的证明方法。那便是引入两个球体，分别在所截平面的上方和下方，并满足这两个球体既与所截平面相切，又与圆锥体相切。

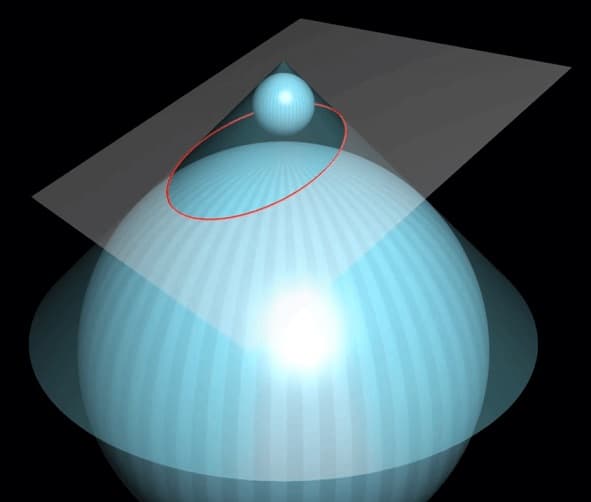
我惊叹于他天才般的构造，在做初中水平的题时，经常喜欢引入一些圆，并利用圆的性质去解题，从而使过程变得简洁而美观。那么丹迪林如何能做到呢？我想除了天赋以外，他的数学思想也贯彻其中：两个球与平面的切点，很可能就是椭圆的焦点。并且如果椭圆上的点到两焦点的距离之和总是相等，那么必然可以利用这两个球，将距离进行某种转换。那么既然这个相交曲线上的点，与焦点的连线必然与球相切，这种转换就应该利用过球外的点做球的切线长总是相等这一结论。由此，我们应该还利用到这“两个球与圆锥体相切”这一条件。

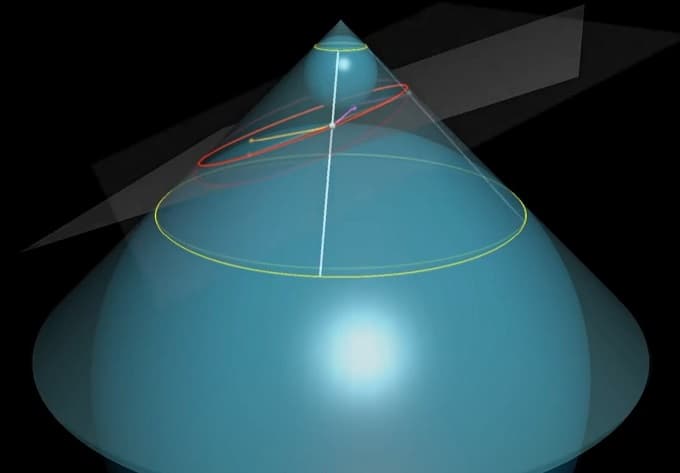
我想这张图已经足够明显，这个证明用到了题设中的所有条件，并且这两个球更使得这个问题直观清晰。若是有人想收集数学中的最美证明，我想它必然当之无愧吧。

不知通过这些问题，读者是否能体会到其中的数学思想。与方法不同，数学思想往往是晦而不显，在平日的做题中，一点一点的积累。我认为化抽象为具体、化未知为已知、化空洞为直观是最常用的思想。通过数学思想的培养，数学的能力才会有一个大幅度的提高。掌握数学思想，就是掌握数学的精髓。