广义相对论中的微分几何引论1

广义相对论中的微分几何引论1

写在前面

微分几何是学习广义相对论的基础，值得注意的是，对于学习物理的学生，与数学的微分几何不太一样，物理中广义相对论需要了解拓扑空间，所以将拓扑结构与微分结构融合在一起讲，而在数学上拓扑学与微分几何则是两门课。 尽管物理上有些定义不如数学书中严密，且物理上同时学习二者难免过于抽象，在梁灿彬的《微分几何与广义相对论》的视频教学影像中，这门课开的很早（大概本科二年级就开了这门课），我喜欢学生们尽早理解物理定律，但从第一节课的人满为患，到第四节课留下来的屈指可数的精英们，能够明显的看出来，很多人被微分几何劝退了……

尽管梁佬的书籍不惜笔墨写了很多叙述，我还是尝试着为基础薄弱的学生提供一种新的理解方式，本文将通过图片配合物理直观的方式降低微分几何的难度，尽管这在一定程度上降低了严谨性，但我相信有此基础，再读广义相对论中涉及的微分几何可能会更快的融入并且上手。

集合与映射

霍金出版了时间简史后又出版了插图版，普及版。因为图片是抽象中直观的东西，本文亦打算如此。首先微分几何第一课让我们重新复习集合论中的东西，而数学则是要重新复习向量的知识，这二者中没有特别难的内容。很多时候画画韦恩图更好一点。

一个花括号中用逗号隔开元素，一个集合诞生了，用韦恩图表示：

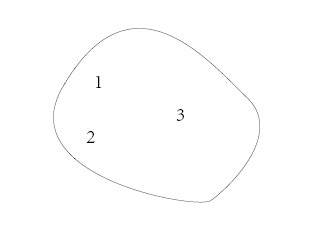
这很好理解，用韦恩图再来考虑De Morgan（德·摩根）定律：

$A-(B \cup C)=$ $(A-B) \cap (A-C)$

只需要随意的画出A,B,C,就能直观的看出结论：

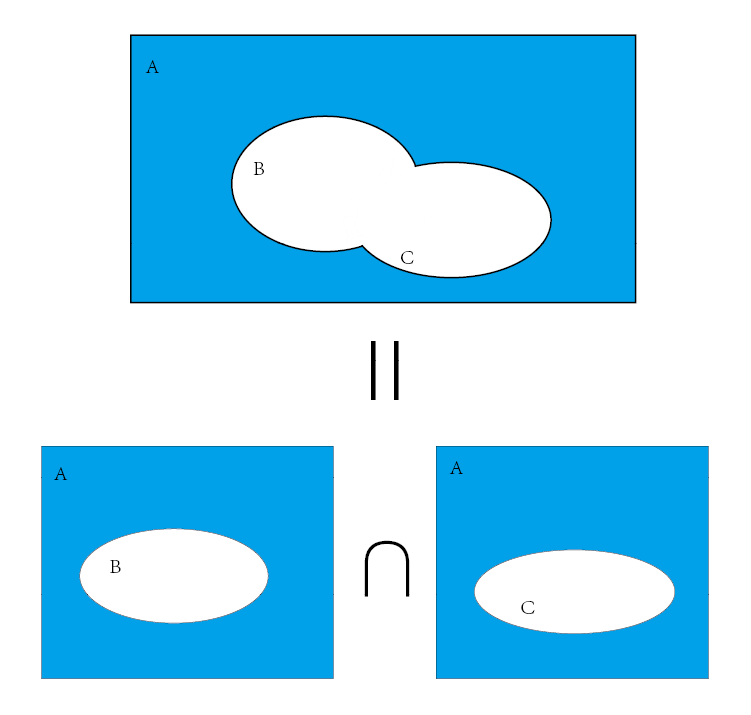
先假设几个一般的A,B,C集合，De Morgan定律无非是告诉我们上者的蓝色部分等于下者蓝色部分叠加，尽管文字证明本定律也并不难。有这种图片直观，即可缓慢培养抽象思维。譬如熟练后给我们一个拓扑空间，我们能在头脑中想象它的大概形状，对于抽象的，不必具体想象它们的形状，只知道有这么个形状就好。

映射，映射是抽象的语言，其实说白了就是一种函数关系，不再说 $y=f(x)$ ，而是用 $f: x \rightarrow y$ 这种新的，抽象的符号语言，这种新的符号语言没有直接给出具体的函数关系，所以这样的好处之一是便于推广（因为没有描述具体怎样，所以更方便加东西上去，我们就可以说，便于推广。）需要注意的是 $f:X \rightarrow Y$ 是集合与集合的映射（指明了一范围），而 $f:x \rightarrow y$ 则表示元素与元素之间的映射（一个元素对应一个元素），一般集合之间的映射用大写英文字母表示，元素之间的映射用小写字母表示，本文也将一直采用此方法，大小写分明，为了加强它们的区别也可将 $f:X \rightarrow Y$ 写作 $f:X \mapsto Y$。 函数有反函数，类似的，映射也有逆映射。用表示 $f^{-1}$ ，这种表示方法与微积分类似。

为了更仔细的说明映射，我们以一段一元函数为例：

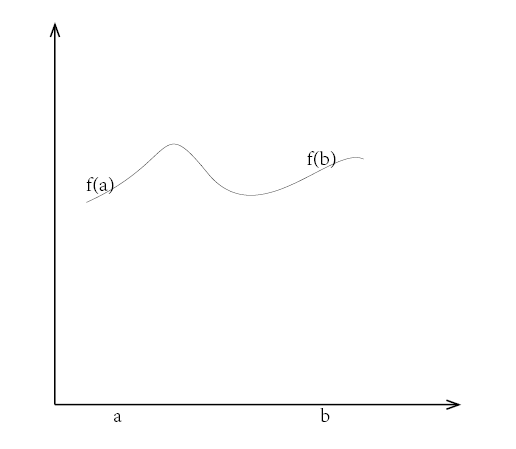
这段函数就是映射下的像，而不再用函数表示，当给出一点 $a$ ，我们知道存在一个映射，把 $a$ 映射到 $f(a)$ 上，而逆像，给出一点 $f(a)$ ，存在一个映射，把 $f(a)$ 映射到 $a$ 上。复变函数里也有一种映射，复数球 到 复平面 上的映射，我们简单的说这种映射关系，就是将圆环面上的点映射到数轴上，如图：

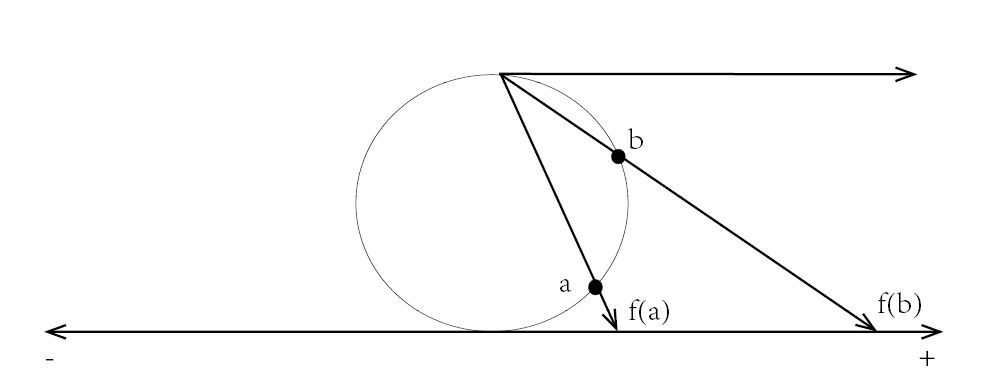
这样圆环面上的点与数轴 一一对应起来，然而在无限远处失去了意义，同样的，我们把圆环面换成球面，数轴换做平面，除了无穷远处，依然可以一一 对应起来。如图：

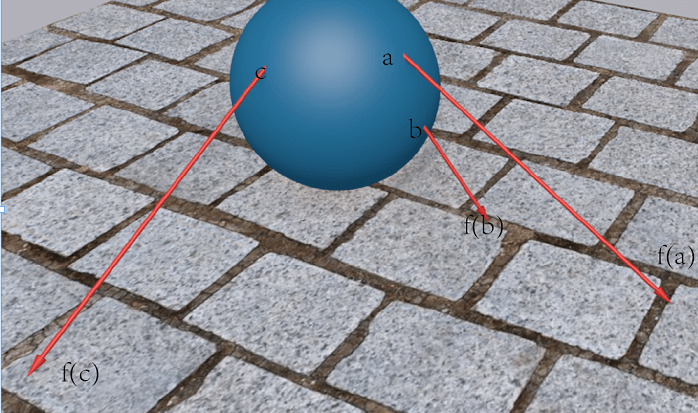
这样，顺理成章有 "一一" 与 "到上" 两个概念：

一一(对应)：若任一 $y \in Y$ 有不多于一个逆像，则称映射 $f:X \rightarrow Y$ 叫 一一 的，或者叫一一(对应)的（集合Y中的某元素 “$y$ ”一个点对应集合X的某元素 “$x$ ”的一个点或者 $0$ 个点）。

到上：若任一 $y \in Y$ 都有逆像，则称映射 $f:X \rightarrow Y$ 叫 到上 的（集合Y中所有的元素 “$y$ ”，在集合X中至少有一个对应元素 “$x$ ”）

通俗的说，就是我们常说的 $x$ 到 $y$ 上的……，进阶版语言 ：$x$ 一一到 $y$ 上的 。而对于连续性的概念：

若 $Y$ 中

任一开区间的逆像都是 $X$ 的开区间之并，则称映射 $f:X \rightarrow Y$ 叫连续的。

这是一元的情况，二元我们可以说是开圆盘之并，三元我们可以说是开球之并，直至向上继续推广。

并且等同于微积分中 $\varepsilon -\delta$ 的连续性定义（$\forall \varepsilon >0$ ，$\exists \delta>0$ ，当 $|x-x_0| < \delta$ 时，有 $|f(x)-f(x_0) |$ $< \varepsilon$ ），如图：

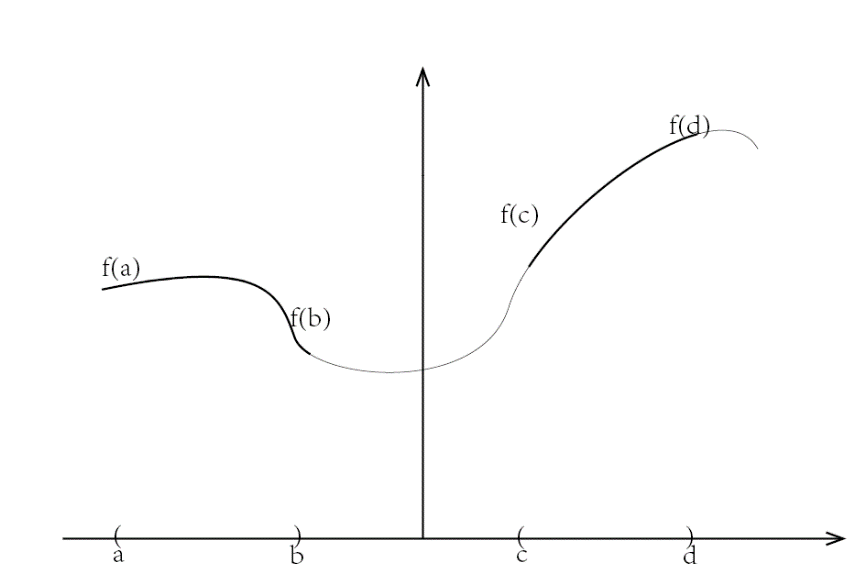
（粗实线部分连续，逆像（a，b）和（c，d）是开区间的并集）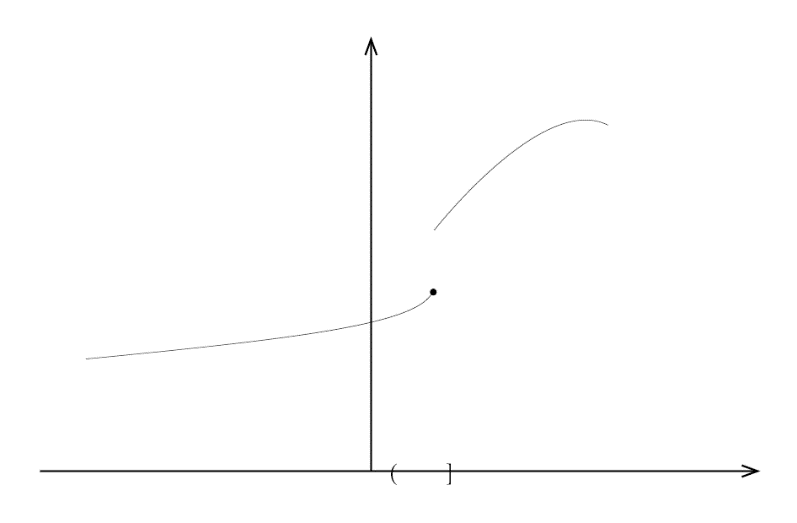

（函数不连续，有一段不是开集）

今天就先到这里，下一期预告：拓扑空间与微分流形。