二次函数

二次函数

定义

形如 $y=ax^2+bx+c$ ( $a,b,c$ 是常数，且 $a \ne 0$ ) 的函数，叫做二次函数(quadratic function) .

二次函数的图象叫做抛物线(parabola)，二次函数 $y=ax^2+bx+c$ 的图象叫做抛物线 $y=ax^2+bx+c$.

抛物线关键词：开口方向、对称轴、顶点.

顶点式

设二次函数 $y=ax^2+bx+c$ 的顶点为$(x_0,y_0)$ ,则有：

$x_0=-\dfrac{b}{2a}$

$y_0=-\dfrac{b^2 -4ac}{4a}$

将二次函数 $y=ax^2+bx+c$ 变形为 $y=a(x-h)^2 +k$ ，称为二次函数的顶点式，其顶点为 $(h,k)$

二次函数 $y=ax^2+bx+c$ 的顶点式推导过程：

$y=ax^2+bx+c$

$= a \left( x^2 +\dfrac{b}{a} x +\dfrac{c}{a} \right)$

 (这一步是提出a，而不是除以a)

$=a$ $\LARGE{\lbrack}$ $x^2$ $+2 \cdot \dfrac{b}{2a} x$ $+\left( \dfrac{b}{2a} \right)^2$$- \left( \dfrac{b}{2a} \right)^2$$+\dfrac{c}{a}$ $\LARGE{\rbrack}$

(加上一次项系数一样的平方 $\left( \dfrac{b}{2a} \right)^2$， 再减去 $\left( \dfrac{b}{2a} \right)^2$，确保代数式的值不变.)

$=a \left( x+\dfrac{b}{2a} \right)^2 - \dfrac{b^2 -4ac}{4a}$

交点式

由于从 $y=a(x-x_1)(x-x_2)$ $(a \ne 0)$ 中可直接看出抛物线与 $x$ 轴的两个交点的坐标 $(x_1,0)$ 、$(x_2,0)$ ，所以通常把 $y=a(x-x_1)(x-x_2)$ 叫做二次函数的交点式.

性质

二次函数 $y=ax^2+bx+c$ 有以下性质：

A. $a>0$ 时抛物线开口向上

B. $|a|$ 越大，抛物线开口越小

C. $b^2-4ac$ 等于0时，与x轴有一个交点，大于0时有两个交小，小于0时无交点

D. $c=0$ 时抛物线过原点

E. $b=0$ 时抛物线对称轴为 $y$ 轴

F. $ab>0$ (即$a$ 、$b$ 同号)时，对称轴在$y$ 轴左侧

G. $ab<0$ (即$a$ 、$b$ 异号)时，对称轴在$y$ 轴右侧

H. $c>0$ 时抛物线与$y$ 轴的正半轴相交

I. $c<0$ 时抛物线与$y$ 轴的负半轴相交

例

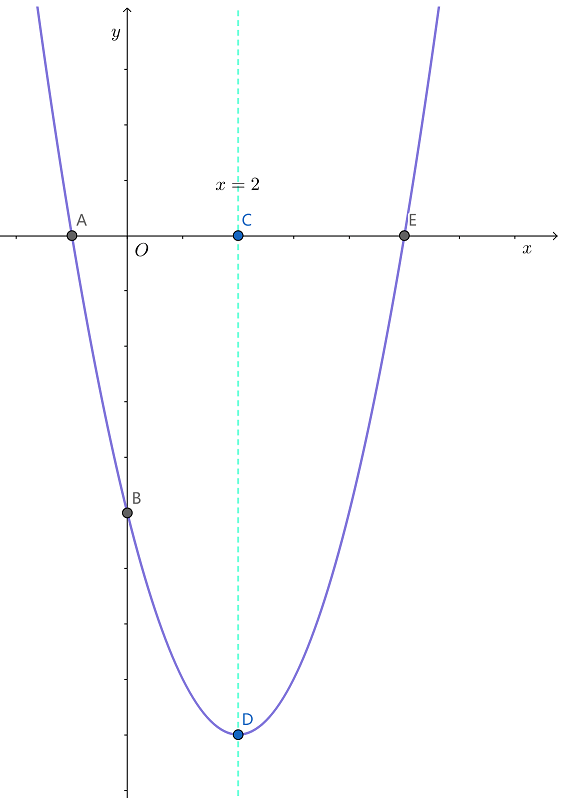
下图是二次函数 $y=x^2-4x-5$ 的图象，其 $a=1$，大于0，开口向上，对称轴 $y= - \dfrac{b}{2a}$ $= -\dfrac{-4}{2}$ $=2$ .