求极限时为什么能消去公因子？

来讲一下求极限时为什么可以消去公因子.

例如计算

$\lim\limits_{x \to 2} \dfrac{x^2-x-2}{x^2-2x}$

我们不能代入 $x=2$ ，因为代入后分子分母都为 $0$ ，对于 $\dfrac{0}{0}$ 型，常用洛必塔法则，对分子分母求导后再求极限.

本题中分子分母有公因子 $(x-2)$ ，消去 $(x-2)$ 后得到了$x \ne 2$ 时和原分式取同样值的更简单的分式：

$\dfrac{x^2-x-2}{x^2-2x}$ $=\dfrac{(x+1)(x-2)}{x(x-2)}=$ $\dfrac{x+1}{x}$

利用这个更简单的分式，我们用代入法求 $x \to 2$ 时的极限为

$\lim\limits_{x \to 2} \dfrac{x+1}{x}$ $=\dfrac{2+1}{2}=1.5$

函数 $\dfrac{x^2-x-2}{x^2-2x}$ 在 $x=2$ 处没有定义，为什么能不顾及没有定义而用消去的方法计算极限呢？可以从图形上分析.

以下是函数

$y=\dfrac{x+1}{x}$

的图形：

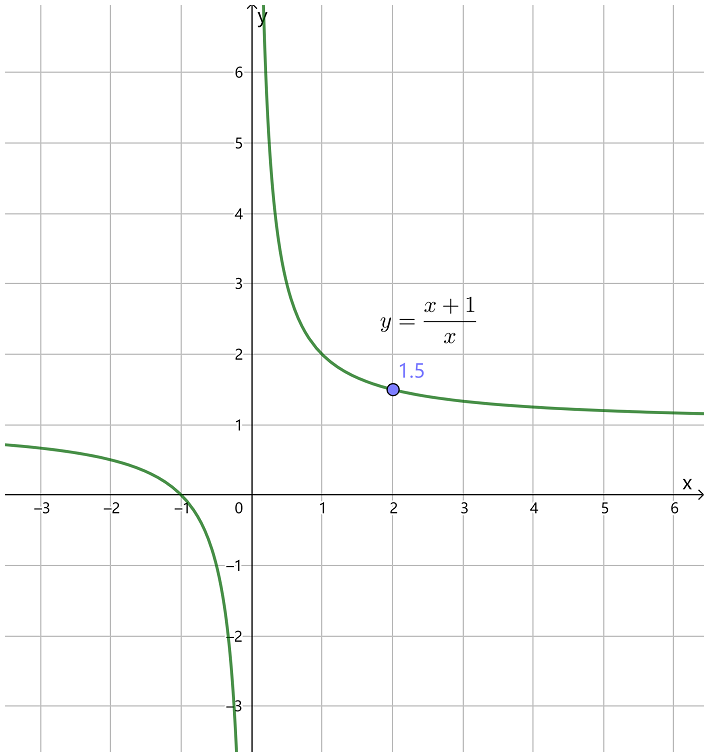
在 $x \to 2$ 时极限为 $1.5$ .

而函数

 $y=\dfrac{x^2-x-2}{x^2-2x}$

的图形与上图很像：

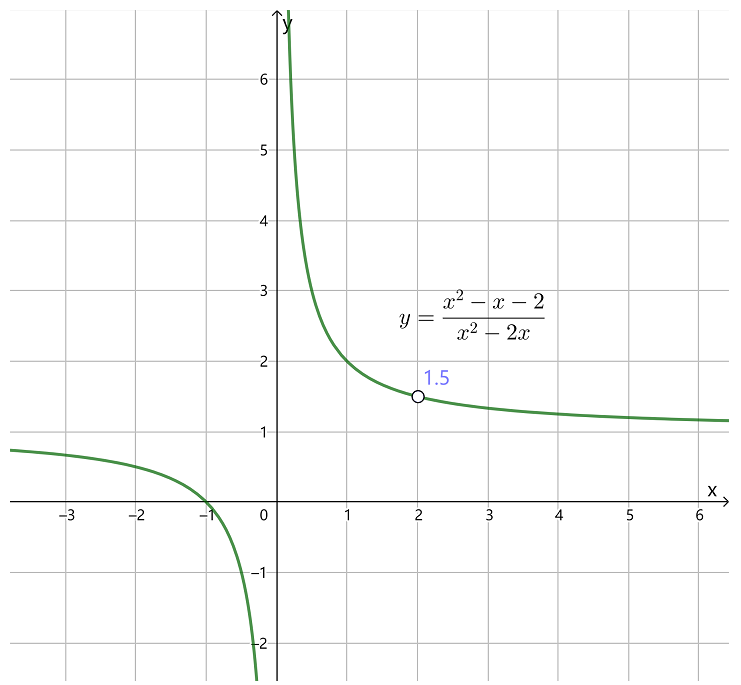
在 $x \to 2$ 时其两个单侧极限，左极限和右极限相等，都等于$1.5$ ，因此可以直接消去公因式.