莱洛三角形

莱洛三角形

Reuleaux triangle

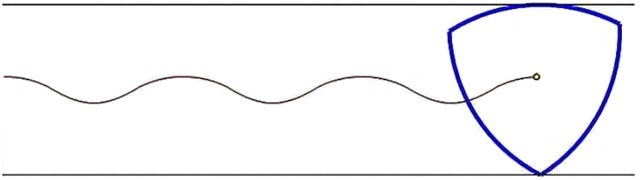
莱洛三角形(Reuleaux triangle)是一种定宽曲线. 其做法为：分别以等边三角形ABC的三个顶点为圆心，以边长为半径做圆，得到如下图的封闭图形.

定宽曲线(Curve of constant width)，或称恒宽曲线，其定义为：平面上一凸形封闭曲线，不论如何转动，其宽度永远不变.

这里所称的 "宽度" 是指平行线 "夹住" 某封闭曲线时，平行线间的距离，所谓 "夹住" 是指每个平行线与凸形封闭曲线相交至少一点且与凸形封闭曲线围起来的内部区域不相交. 或者说，将一个闭合曲线 (圆或莱洛三角形) 放在两条平行线中间，使之与这两平行线相切，可以做到：无论这个闭合曲线如何运动，只要它仍与原平行线中的一条直线相切，就必与另一条直线线相切，那么此闭合曲线为定宽曲线.

另一种定宽曲线是圆.

莱洛三角形由德国人Franz Reuleaux（1829～1905）发现并以他的命字命名. Franz Reuleaux 发明了300多种机械模型，被誉为动力学（kinematics）之父.

下图是莱洛三角形的一个应用：一个没有活塞的、转子形状是莱洛三角形的发动机气缸.

image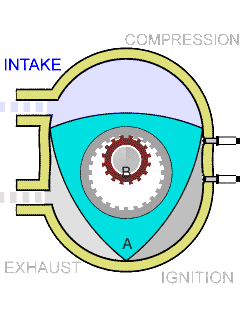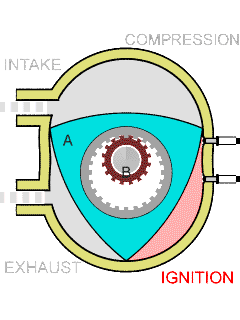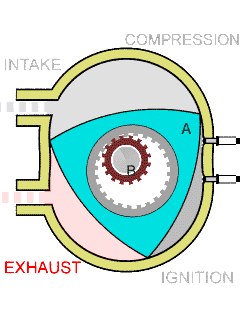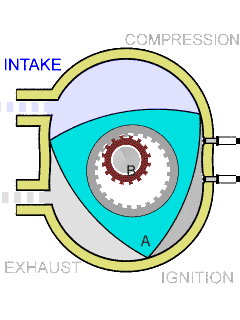

下图是莱洛三角形的另一个应用：在零件上打方形孔.

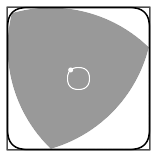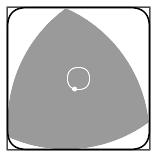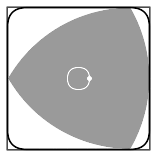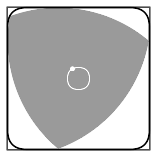
下图是它的第三个应用，这也是所有定宽曲线的特性：用它们做下水道井盖不会掉入下水道.

但莱洛三角形不适合用来做车轮，莱洛三角形转动时它的中心会上下摆动，如下图：