高中集合的一些概念

高中集合的一些概念

先重点

子集个数：由 $n$ 个元素组成的集合 $A$ 有 $2^n$ 个子集，$2^n -1$ 个真子集.

并集和交集记忆方法 ：

并集 $\cup$ ，向上开口，像个正立的杯子，想像向里倒水，则水都收集起来，用以辅助理解并集是将两个集合汇集起来（越来越多）。

交集 $\cap$ ，向下开口，像个倒扣的杯子，此时向里倒水，水会分散到两边，用以辅助理解交集是将两个集合公共部分挑出来（越来越少）。

集合的运算律

交换律

$A \cap B = B \cap A$

$A \cup B = B \cup A$

结合律

$A \cap ( B \cap C) =$ $(A \cap B) \cap C$

$A \cup ( B \cup C) =$ $(A \cup B) \cup C$

分配律

$A \cap ( B \cup C) =$ $(A \cap B) \cup$ $( A \cap C)$

$A \cup ( B \cap C) =$ $(A \cup B) \cap$ $( A \cup C)$

德$\cdot$ 摩根定律

 ${\complement}_U (A \cap B)=$ $({\complement}_U A) \cup$$({\complement}_U B)$

 ${\complement}_U (A \cup B)=$ $({\complement}_U A) \cap$$({\complement}_U B)$

再概念

一般地，我们把研究对象统称为元素(element)，把一些元素组成的总体叫做集合(set)，简称为集.

集合中的元素互不相同. 只要构成两个集合的元素是一样的，我们称这两个集合是相等的.

常用大写拉丁字母 $A,B,C, \cdots$ 表示集合，用小写拉丁字母 $a,b,c,\cdots$ 表示集合中的元素. 如果 $a$ 是集合 $A$ 的元素，就说 $a$ 属于(blong to)集合 $A$ ，记作 a∈A；如果 $a$ 不是集合 $A$ 中的元素，就说 $a$ 不属于(not blong to)集合$A$ ，记作$a \notin A$ .

集合的表示方法：列举法、描述法、Venn图、区间法

列举法：把集合的元素一一列举出来并用花括号“{ }”括起来表示集合的方法. 如$A= \{ 1,2,3 \}$ 、$B= \{ x=2$ $,y=3,z=4 \}$

描述法: 用集合所含元素的共同特征表示集合的方法. 如$C= \{ x \in \bold{Z} | x>10 \}$ ，如果从上下文的关系来看，$x \in \bold {R}, x \in \bold {Z}$ 是明确的，那么$x \in \bold {R}, x \in \bold {Z}$ 可以省略，只写其元素x. 例如，集合 $D=\{ x \in \bold {R} |$ $x<10 \}$ 也可以表示为$D=\{ x | x<10 \}$ ; 集合 $E=\{ x \in \bold {Z}$$| 2k+1, k \in \bold {Z} \}$ 也可以表示为$E=\{ x | 2k+1$ $, k \in \bold {Z} \}$ .

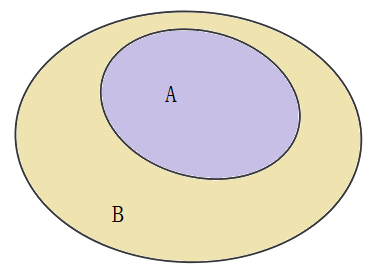
Venn图：集合的第三种表示方式，用平面上封闭曲线的内部代表集合的图称为Venn图. 下图表示集合A和集合B的包含关系.

区间法，是集合的第四种表示方式. 设a,b是两个实数，且 $a<b$ ，规定：

1）闭区间：满足不等式 $a \leqslant x$ $\leqslant b$ 的实数 $x$ 的集合叫做闭区间，表示为 [a,b]；

2）开区间：满足不等式 $a < x < b$ 的实数 $x$ 的集合叫做闭区间，表示为 (a,b)；

3）半开半闭区间：满足不等式 $a \leqslant x < b$ ，$a < x \leqslant b$ 的实数 $x$ 的集合叫做半开半闭区间，表示为 [a,b)，(a,b]；

这里的实数 a 与 b 都叫做相应区间的端点，a为左端点，b为右端点，称 $b-a$ 为区间长度.

子集(subset)：对于两个集合A、B，如果集合A中任意一个元素都是集合B中的元素，就说这两个集合有包含关系，称集合A为集合B的子集同，记作 $A \subseteq B$ 或 $B \supseteq A$ ，读作“A含于B” 或 “B包含A”

相等：如果集合A是集合B的子集($A \subseteq B$ )，且集合B是集合A的子集($B \subseteq A$ )，此时，两个集合中的元素是一样的，称集合A与集合B相等，记作A=B

真子集(proper subset)：如果集合$A \subseteq B$ ，但存在元素$x \in B$ ，且$x \notin A$ ，称集合A是集合B的真子集，记作A⫋B 或$B \supsetneqq A$ .

空集(empty set)：不含任何元素的集合叫做空集，记为 $\varnothing$ ，并规定：空集是任何集合的子集.

并集(union set)：由所有属于集合A或属于集合B的元素组成的集合，称为集合A与集合B的并集，记作$A \cup B$ ，读作 “A并B”，即

$A \cup B = \{ x | x \in A,$ 或 $x \in B \}$

交集(intersection set)：由属于集合A且属于集合B的所有元素组成的集合，称为A与B的交集，记作 A∩B，读作 “A交B”，即

$A \cap B = \{ x | x \in A,$ 且 $x \in B \}$

全集(universe set)：含有我们所研究问题中涉及的所有元素的集合，通常记作U .

补集(complementary set)：对于一个集合A，由全集U中不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集，简称为集合A的补集，记作 ${\complement}_U A$ 即

${\complement}_U A = \{ x | x \in U,$ 且$x \notin A \}$