分项分式积分法

分项分式积分

微积分处理技巧之一

z张z

首先简单介绍一下长除法，它用来处理高次幂多项式除低次幂多项式，或者说有理函数多项式，目的是让分子次数小于分母。如计算

$\int \frac{x^{3}-x^{2}+x+4}{x+1} d x$ ，这里 $\frac{x^{3}-x^{2}+x-4}{x+1}$ 通常用长除法，也就是我们小学学过的除法。

长除法

步骤如下：

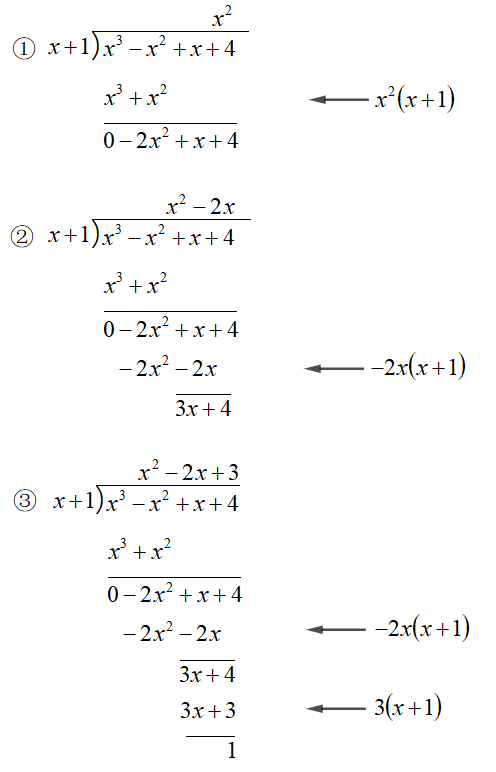
余式次数小于除式次数，可以停止运算。

也就是说

$\frac{x^{3}-x^{2}+x+4}{x+1}$ $=x^{2}-2 x+3+\frac{1}{x+1}$

这样它的积分

$\int x^{2}-2 x+3+\frac{1}{x+1} d x$

也便好算了。

需要注意的是，做长除法分子分母次数由高到低排列，像 $x^{4}+x^{2}$ ，按照 $x^{4}+0 x^{3}+x^{2}$ 排列来除。

部分分式

高中时我们知道 $\frac{1}{n(n+k)}$ $=\frac{1}{k}\left(\frac{1}{n}-\frac{1}{n+1}\right)$ 参见〖裂项相消法1〗，但是形如 $\frac{f(x)}{n(n+1)}$ 的分式需要更进一步的方法，也就是 [部分分式分解]

定理：任何一个真分式 $\frac{P(x)}{Q(x)}$ ，都可以分解成若干个简单分式之和。

简单分式大多是这几种类型：

$\frac{A}{x+a}$ ，$\frac{A}{(x+a)^{k}}$ ，$\frac{A x+B}{x^{2}+p x+q}$ ，$\frac{A x+B}{\left(x^{2}+p x+q\right)^{k}}$

直接给出几种常用的一般做法：

1、$\frac{p x+q}{(x+a)(x+b)}$ $\Leftrightarrow$ $\frac{A}{x+a}+\frac{B}{x+b}$ （$a \ne b$ ）

2、$\frac{p x+q}{(x+a)^{2}}$ $\Leftrightarrow$ $\frac{A}{x+a}+\frac{B}{(x+a)^{2}}$

3、$\frac{p x^{2}+q x+r}{(x+a)(x+b)(x+c)}$ $\Leftrightarrow$ $\frac{A}{x+a}+\frac{B}{x+b}+\frac{C}{x+c}$

4、$\frac{p x^{2}+q x+r}{(x+a)(x+b)^{2}}$ $\Leftrightarrow$ $\frac{A}{x+a}+\frac{B}{x+b}+\frac{C}{(x+b)^{2}}$

5、$\frac{p x^{2}+q x+r}{(x+a)\left(x^{2}+b x+c\right)}$ $\Leftrightarrow$ $\frac{A}{x+a}+\frac{B x+C}{x^{2}+b x+c}$ （$x^{2}+b x+c$ 不能再分解）

A、B、C都是常数可以通过通分求出，其实还有几种不常见的形式，暂不列出。

分式分项积分

比如计算 $\int \dfrac{1}{1+x^{3}} d x$ （其实本来想用 $\dfrac{1}{1+x^{4}}$ 来说明）

将 $\dfrac{1}{1+x^{3}}$ 分母分裂

$\dfrac{1}{1+x^{3}}=$ $\dfrac{1}{(x+1)\left(x^{2}-x+1\right)}$ ，它是上面提到的第5种形式，故

$\dfrac{1}{(x+1)\left(x^{2}-x+1\right)}$ 可以写成 $\dfrac{A}{x+1}+\dfrac{B x+C}{x^{2}-x+1}$ ，通分得到算式

$A\left(x^{2}-x+1\right)$ $+(B x+C)(x+1)$ $=1$

即

$(A+B) x^{2}$ $+(B+C-A) x$ $+A+C=1$

$A+B=0$ ,

$B+C-A=0$ ,

$A+C=1$ ,

解出：$A=\frac{1}{3}$ ，$B=-\frac{1}{3}$ ，$C=\frac{2}{3}$

所以：

$\int \frac{1}{(x+1)\left(x^{2}-x+1\right)} d x$ $=$ $\frac{1}{3} \int \frac{2-x}{x^{2}-x+1} d x$ $+\frac{1}{3} \int \frac{1}{x+1} d x$

把一个积分换成两个小积分，这样它的积分便好算了，其实有更快的算待定系数A,B,C的方法，这里我卖一个关子，希望读者做题探索。

最后提一下形如 $\frac{P(x)}{[Q(X)]^{k}}$ 的部分分式，其中 $P(x)$ 次数是小于 $Q(x)$ 的多项式，且 $\frac{P(\mathrm{x})}{Q(\mathrm{x})}$ 是 [既约真分式] 则

$\frac{P(x)}{[Q(x)]^{k}}=$ $=\sum_{i=1}^{l} \sum_{k_{i}=1}^{k} \frac{P_{i} k_{i}(x)}{[Q(x)]^{k_{i}}}$

其中 $P_{i} k_{i}(x)$ 的次数小于 $Q(x)$ 的次数。

用一个简单的例子理解这句话就是：

$\dfrac{x^{2}+3 x-1}{x^{3}+6 x^{2}+12 x+8}$

$=$ $\dfrac{x^{2}+3 x-1}{(x+2)^{3}}$

$=$ $\dfrac{1}{x+2}-\dfrac{1}{(x+2)^{2}}$ $-\dfrac{3}{(x+2)^{3}}$

本文完。