月明中讲复变函数（四）

不知道复变函数有什么用？知道黎曼猜想吗？如果想看懂这一猜想，需要先懂复变函数.

复变函数（四）

数学长征，月明中

复数的模与辐角：表示复数 $z$ 的位置，也可以借助于于点z的极坐标 $r$ 和 $θ$ 来确定（图1）.

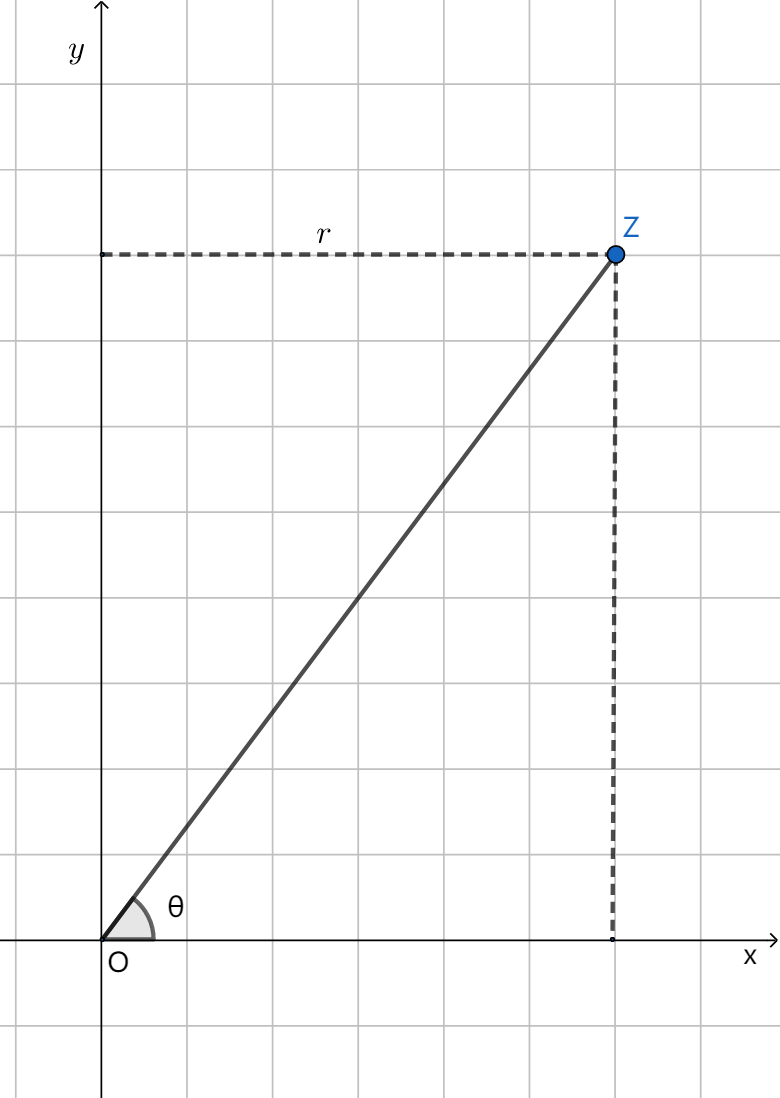
图1

上节我们用向量 $OZ$ 来表示复数 $z=x+iy$ ，其中 $x$ ，$y$ 顺次等于$OZ$ 沿 $x$ 轴与 $y$ 轴的分量. 向量 $OZ$ 的长度称为复数 $z$ 的模或绝对值，以符号 $|z|$ 或 $r$ 表示，因而有 $r=|z|$ $=\sqrt{x^2+y^2}$ $\geqslant 0$ , 且 $|z|=0$ 的充要条件是 $z=0$ .

这里引进的模的概念与对于实数的绝对值的概念是一致的.由于复数z的模|z|是非负实数，所以能够比较大小.

根据图1我们有不等式

$|x| \leqslant |z|$ ，$|y| \leqslant |z|$ ，$|z| \leqslant |x|+|y|$

根据图2我们有不等式

$|z_1+z_2| \leqslant |z_1|+|z_2|$ (三角形两边之和大于第三边)

它称为三角不等式.

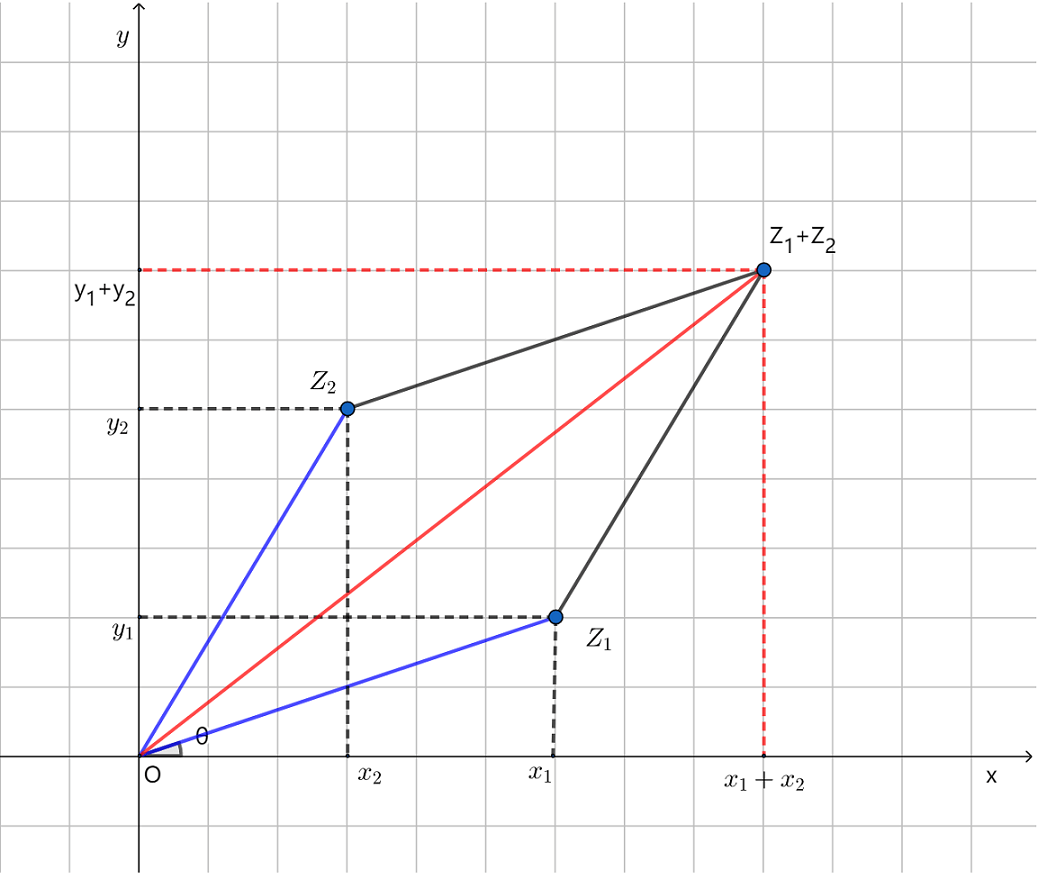
图2

此外，根据图3，我们还有不等式

$||z_1|-|z_2||$ $\leqslant |z_1|-|z_2|$ (三角形两边之差小于第三边)

等号成立的几何意义是复数$z_1$ ，$z_2$ 所表示的两个向量共线且同向.

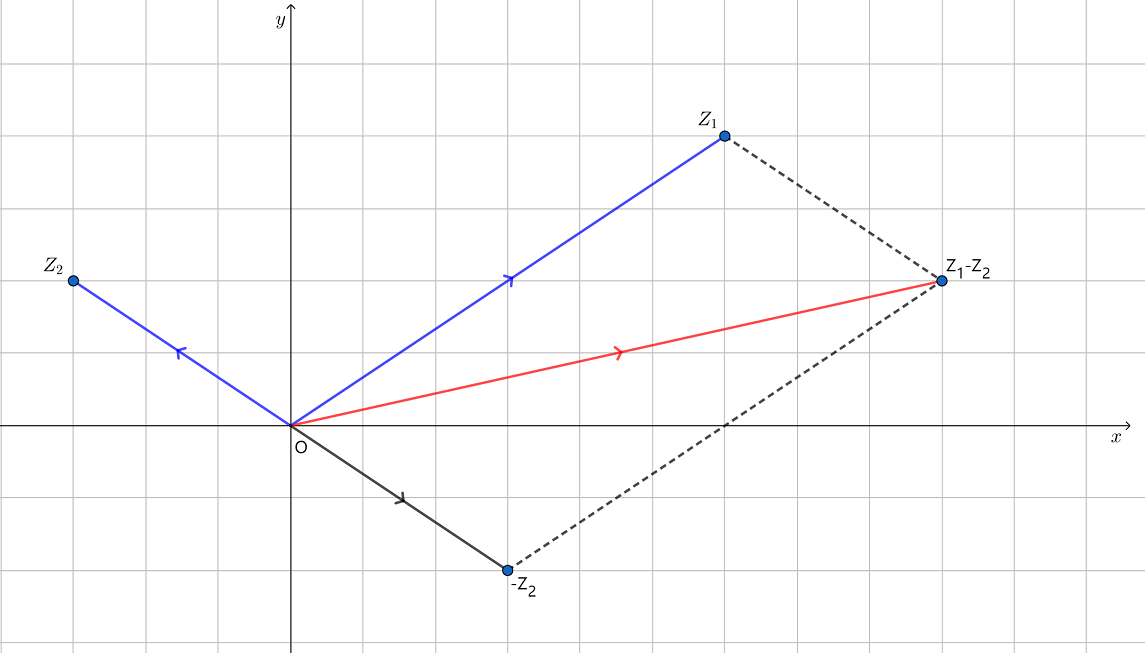
图3

由图3可见，$|z_1-z_2|$ 表示点 $z_1$ 与点 $z_2$ 的距离，记为

$d(z_1,z_2)$$=|z_1-z_2|$

ニ复数差的模的这个几何意义是非常重要的. 它还可以借助解析几何中两点间的距离公式用解析方法得出：

$|z_1-z_2|=$$|(x_1+iy_1)-(x_2+iy_2)|$ $=\sqrt{(x_1 -x_2)^2 + (y_1 -y_2)^2}$

实轴正向到非零复数 $z=x+iy$ 所对应的向量 $OZ$ 间的夹角θ合于

$\tan \theta= \dfrac{y}{x}$ ，

称为复数 $z$ 的辐角，记为

$\theta =Argz$ .

我们知道，任一非零复数 $z$ 有无穷多个辐角，现以argz表示其中一个特定值，并称合条件

$-\pi <argz < \pi$

的一个为 $Argz$ 的主值，或称之为 $z$ 的主辐角.

于是 $\theta =Argz$ $=argz +2k \pi$ $(k \in \bold Z)$

注意：当 $z=0$ 时，辐角无意义.