月明中讲复变函数（三）

不知道复变函数有什么用？知道黎曼猜想吗？如果想看懂这一猜想，需要先懂复变函数.

复变函数（三）

数学长征，月明中

一个复数 $z=x+iy$ 本质上由一对有序实数$(x,y)$唯一确定. 于是能够建立平面上全部的点和全体复数间一一对应的关系。换句话说, 我们可以借助于横坐标为 $x$ ，纵坐标为 $y$ 的点来表示复数 $z=x+iy$ (图1).

由于 $x$ 轴上的点对应着实数，故 $x$ 轴称为实轴；$y$ 轴上的非原点的点对应着纯虚数，故 $y$ 轴称为虚轴，这样表示复数 $z$ 的平面称为复平面或 $z$ 平面.

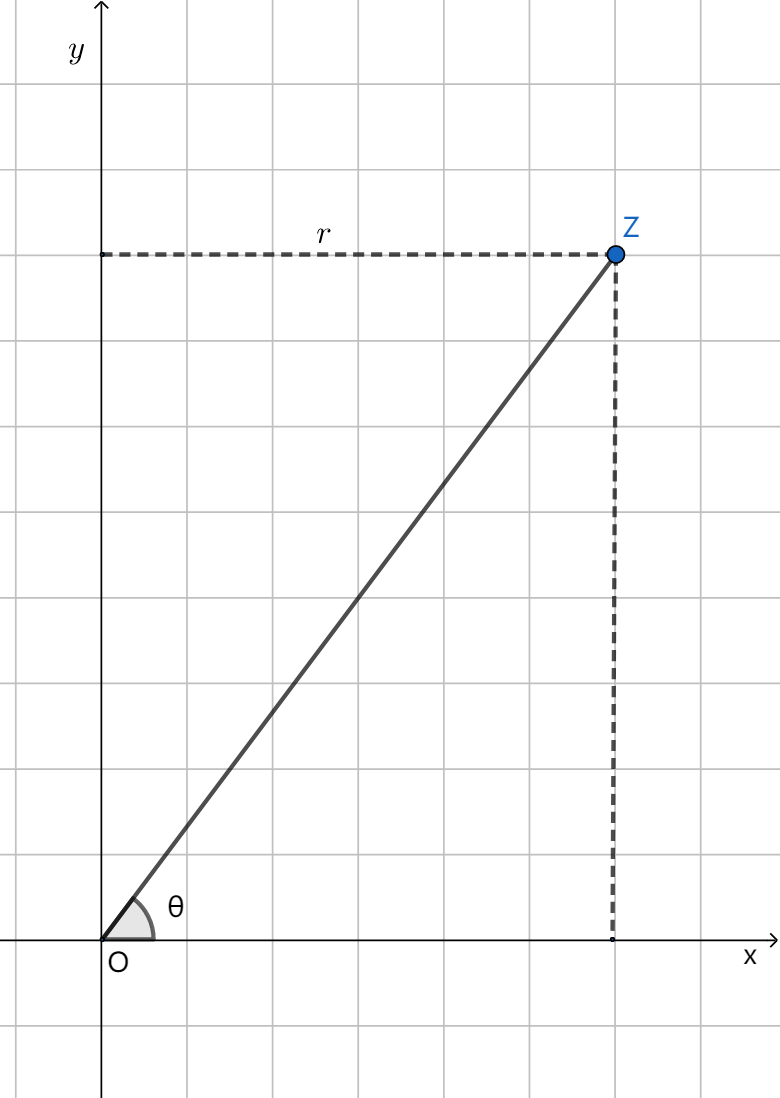
图1

引进了复平面之后，我们在「数」和「点」之间建立了联系. 以后在研究复变函数时，常可借助于几何直观，还可采用几何术语. 这也为复变函数应用于实际提供了条件，丰富了复变函数论的内容. 为了方便起见, 今后我们不再区分「数」和「点」、「数集」和「点集」，说到「点」可以指它所代表的「数」，说到「数」也可以指这个数代表的「点」. 例如，我们常说「点$1+i$ 」,「顶点为$z_1$ ，$z_2$ ，$z_3$ 的三角形」等等.

在复平面上，从原点到点 $z=x+iy$ 所引的向量与这个复数$z$ 也构成一一对应关系（复数$0$ 对应着零向量）. 这种对应关系使复数的加减法与向量的加减法之间保持一致.

例如, 设：

$z_1= x_1+ iy_1$ , $z_2=x_2+iy_2$

则

$z_1+z_2=(x_1+x_2)+i(y_1+y_2)$ .

由图2可以看出，$z_1+z_2$ 所对应的向量，就是 $z_1$ 所对应的向量与 $z_2$ 所对应的向量的和向量.

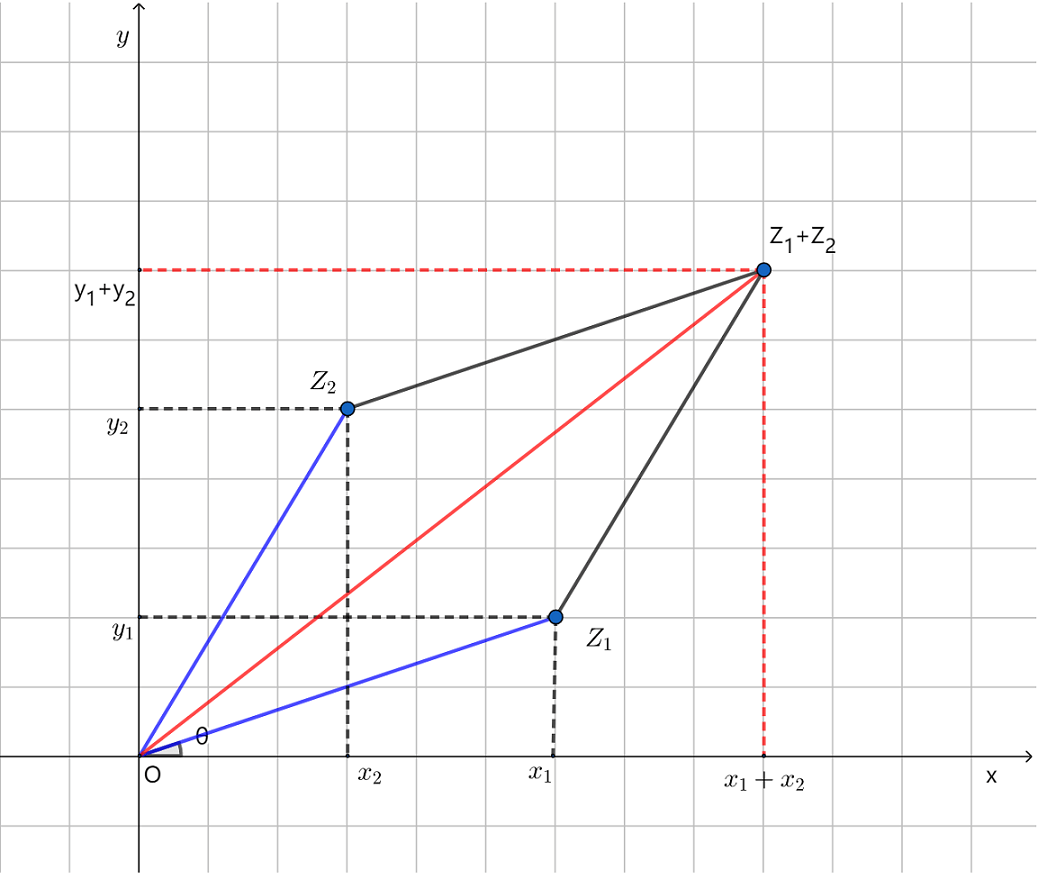
图2

又如，将 $z_1-z_2$ 表示成 $z_1+(-z_2)$ ，可以看出，$z_1-z_2$ 所对应的向量就是$z_1$ 所对应的向量与$(-z_2)$ 所对应的向量的和向量，也就是从$z_2$ 到$z_1$ 的向量，如图3.

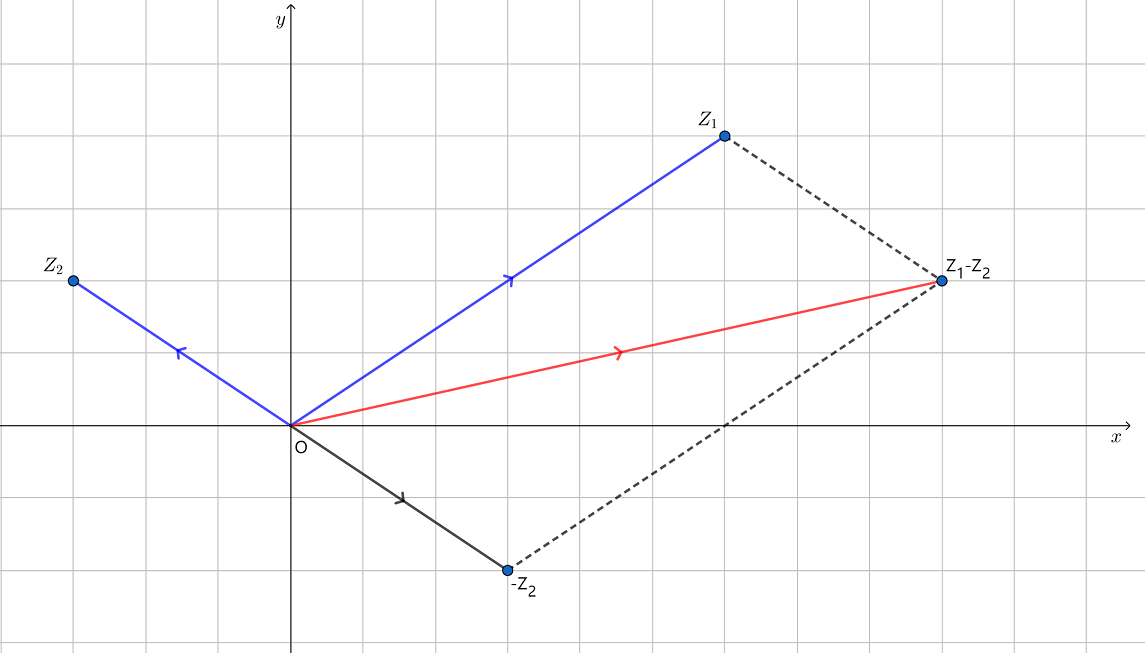
图3