反比例函数与双曲线
反比例函数与双曲线
反比例函数(inverse proportional function)是形如 的函数,其中x是自变量,y是函数,k是常数且不等于0.
反比例函数中, k也称为反比例常数,分母不能是多项式,只能是x的一次单项式,其形式也可以写为 或 ( ) .
成反比例关系的不一定是反比例函数,但反比例函数中的两个变量一定成反比例关系.
一次函数 的图象是一条直线,二次函数 的图象是一条抛物线,反比例函数的图象由两条曲线共同组成,称为双曲线,双曲线的两个分支关于原点对称,如下图。
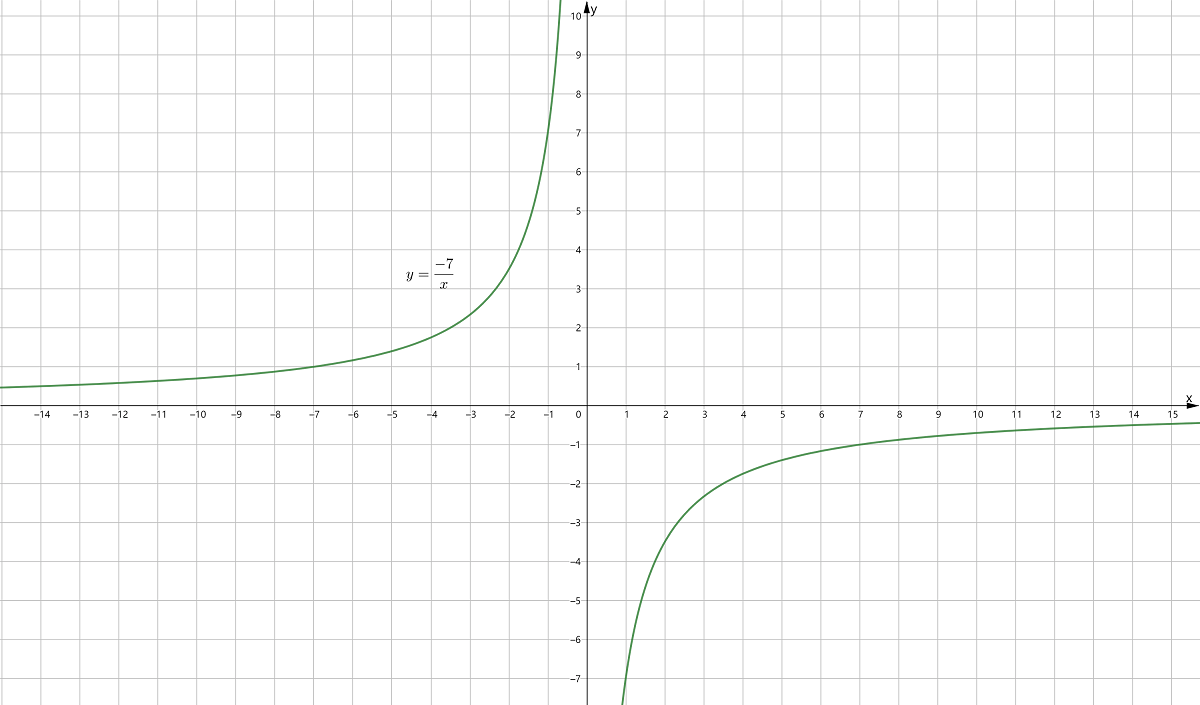
形如 的一次函数也称为正比例函数,其自变量x的取值范围为全体实数,而反比例函数自变量x的取值范围为不等于0的全体实数.
双曲线是由两个分支组成的,一般不说两个分支经过第一、三象限(或二、四象限),而说图象的两个分支分别在第一三象限(或二、四象限).
由于双曲线的图象不是连续的,因此所谈到到的反比例函数的增减性,都是在各自象限内的增减情况. 当K>0时,在每一个象限(第一、三象限)内,y随x的增大而减小,但不能笼统地说当k>0时y随x的增大而减小;同样,当k<0时也不能笼统地说y随x的增大而增大.
随着|x|的增大,双曲线逐渐向坐标轴靠近,但永远不与坐标轴相交,因为反比例函数中 且 .
反比例函数中比例系数k的几何意义是,过双曲线上任意一点做与两条坐标轴垂直的线段,它们与坐标轴围棋的矩形面积恒定为| k |. 如图,在反比例函数 的图象上任取一点P,过P做x轴的垂线并与x轴交于M,过P做y轴的垂线并与y轴交于N,O为坐标原点,则矩形ONPM的面积始终为| K |.
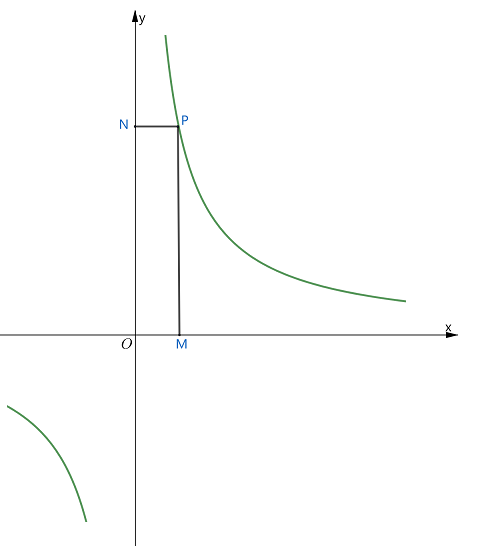
所以,无论P在何处, 或 的面积恒为 .


