点关于直线的反射变换

如下图，设点A的坐标为$(x,y)$ ，做点 $A$ 关于 $y$ 轴的反射变换(对称变换)，得到 $B$ 点 $(x',y')$ ，那么 $B$ 点的坐标为

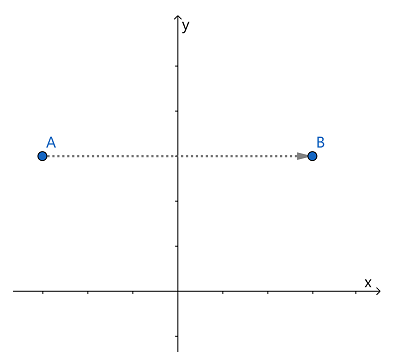
$\begin{cases} x'=-x \\ y'=y \end{cases}$

将上式改写为

$\begin{cases} x'=-x +0y\\ y'=0x+y \end{cases}$

这一变换由上式中右端式子 $x,y$ 的系数唯一确定，把它们按原来的顺序写出来疘两端分别加上一个括号，得到如下的正方形数表

$\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}$

这个正方形数表称为二阶矩阵，把它当作一个计算工具，即从y轴左侧区域向y轴右侧区域做反射变换的计算工具，即用代数方法表示几何变换的工具.

根据以上推出此工具的步骤，用以下二阶矩阵

$\begin{bmatrix} a & b \\ c & d \end{bmatrix}$

计算坐标(x,y)的变换点坐标(x',y')，正确的算法是：

$x'=ax+by$ ,

$y'=cx+dy$ .

点 $P(x,y)$ 关于直线 $Ax+By+C=0$ 反射变换的坐标变换公式

$\begin{cases} x'=x-2At, \\ y'=y-2Bt. \end{cases}$

其中

$t=\dfrac{Ax+By+C}{A^2+B^2}$

由上式推导出点关于直线 $Ax+By=0$ 的反射变换二阶矩阵是

$\begin{bmatrix} \dfrac{B^2-A^2}{A^2+B^2} & -\dfrac{2AB}{A^2+B^2} \\ -\dfrac{2AB}{A^2+B^2} & \dfrac{A^2-B^2}{A^2+B^2} \end{bmatrix}$