青羽讲数学史(一)
青羽讲数学史(一)
数学长征,青羽
为什么需要讲数学史?
在一般人看来,数学是一门枯燥无味的学科,因而很多人视其为畏途。从某方面来说,这是由于我们的教科书上往往只是讲述一些僵化的、一成不变的内容。如果在教学中能渗透数学史从而让数学活化起来,我想这样便可以激发人们对数学的学习兴趣,也有助于人们对数学的理解与认知的深化。
毫不客气地说,科学都是向前看的。每日都有成千上万的新论文产生,但鲜有人会关注过去数学家所做的事。旧理论只是用来开发新理论的工具,而这些工具,也正是我们在学校所学到的。可以说,所有的这些定理都是以一种“结晶态”的形式为我们所知,它们简洁且易于理解,但它们在当时那个年代,可不仅仅是这么简单。数学家在不断完善这些理论的过程中,有些东西蒸发了,有些东西沉淀了,而所有的这些“运动”的动力来源,正是数学家们的思想。
读数学史,有助于研究著名数学家的思想,从中汲取养分,从而古为今用,推陈出新。更重要的是,读数学史很容易开发一个人对数学的兴趣,我也会尽量用轻松诙谐的方式,去为大家打开数学史的大门。
第一章 从毕达哥拉斯到第一次数学危机


一、为什么是毕达哥拉斯?
在古希腊,有很多著名的数学家如阿基米德、欧几里得等。但阿基米德、欧几里得的年代都比毕达哥拉斯的要晚,其思想也深受毕达哥拉斯的启发。在当时,毕达哥拉斯或许称得上是一个新时代的思想家,他既是极富感染力的演说家,也是著名学者,同时还是一位魅力超凡的老师。据说,他还为居住在意大利的希腊人撰写了宪法章程。学生蜂拥而至,毕达哥拉斯的周围迅速聚集了一群想要聆听这位导师教诲的追随者。
毕达哥拉斯认为自己是英雄福尔波斯的转世化身,这一点令他坚信,所有灵魂,包括动物的灵魂,在死后都会轮回转生。因此他是一个严格的素食主义者。但豆子被列为禁忌之物,因为它会引起胃气涨,也因为它们长得很像男性生殖器。
据说毕达哥拉斯有一个滑稽的死法。有一天,毕达哥拉斯的仇人们(毕达哥拉斯认为他们不够富有而拒绝了他们的求见,因此愤恨不已)点火烧了他的房子,当时正在屋内的弟子们四散而逃,紧随其后的暴徒毫不留情地将他们一一屠杀,毕达哥拉斯孤身躲窜逃命,却猛然跑到了一片豆田前。他停下了脚步,因为在他看来,与其穿过这片豆田,还不如就死在这里。尾随者当然十分高兴,欣然抬手就割破了毕达哥拉斯的喉咙。
尽管学派分崩离析,领袖也已经与世长辞,但毕达哥拉斯学派的教义仍未陨灭,其精华仍旧留存于世,并被亚里士多德吸纳。后者的思想理念传世两千多年,成为西方历史上最具影响力的哲学体系。
二、毕达哥拉斯与黄金比例
古希腊人的数学继承自古埃及的几何学,因而在古希腊数学中,图形与数字之间并没有明显的界限,并且在希腊人眼中,哲学家与数学家几乎可视为一体。那时古希腊数学家常通过绘制精密图形来证明某些数学定理,他们手中的工具不是铅笔和纸张,而是直尺与圆规。毕达哥拉斯认为,图形与数字之间的联系高深而神秘,每一个形数背后都有各自隐藏的含义,而最具美感的那个形数则堪称神圣。
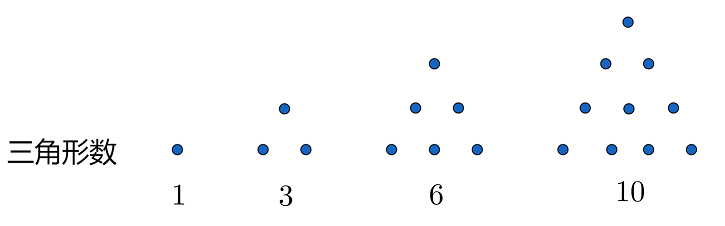
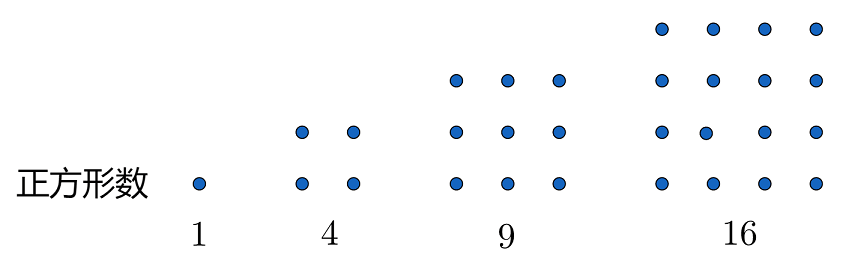
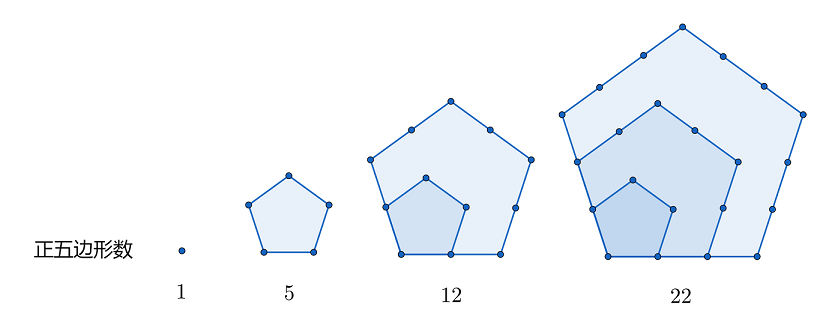
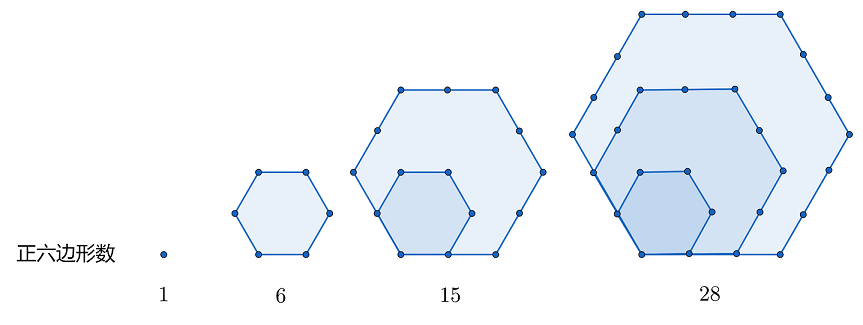
一些形数
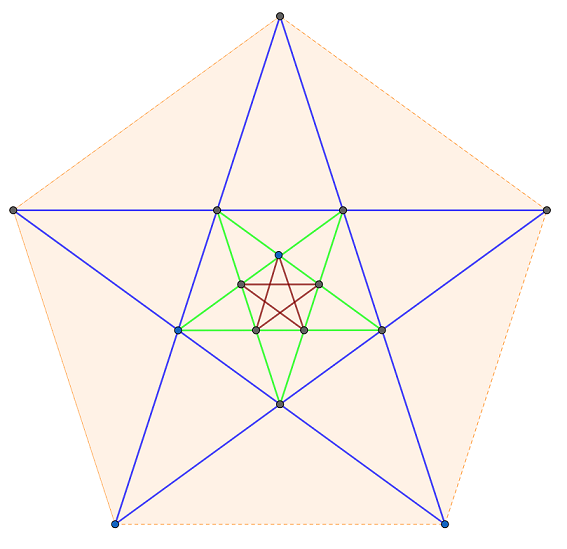
毕达哥拉斯学派有一个神秘标志,这个标志自然是一个形数:一个五角星形。这个图案看似简单,却能窥见无穷。将其各顶点相连可得一个五边形,用直线将此五边形各顶点交叉相连又可得到一个倒置的小五角星,这个小五角星与原来的五角星形状相同,大小成一定比例。这一过程可以无限延续下去,终而复始,循环无端。这种自我复制甚为有趣,但它并不是毕达哥拉斯学派的信徒们关注的焦点,他们认为,这个图形最核心的特质潜藏在五角星的线条之中,这些线条里蕴藏着一个形数,这个形数是毕达哥拉斯学派宇宙观的终极象征——黄金比例(the golden ratio)
据传说,有一天毕达哥拉斯正摆弄一台单弦琴,他注意到,若略微移动琴桥,将琴弦以3:2的比例划分,在此情况下弹拨琴弦,两部分琴弦弹出的音调将合奏出一个纯五度音(perfect fifth)。纯五度是音乐世界中最具感染力、最能唤起共鸣的音程关系。不同比例下的不同和声,或抚慰人心,或叫人心烦意乱(比如,三全音音程就极不和谐,被称为“地狱之音”,为中世纪音乐家所摈弃)。奇怪的是,如果琴桥所处的位置不能讲琴弦分割成一个简单的比例关系(有理数),两边弹奏的音调就无法和谐,往往刺耳难耐,甚至更糟。此时奏出的和声摇移不定,就像一个喝醉了在音阶上东倒西歪的酒鬼。
对于毕达哥拉斯来说,音乐是一项数学行为,线条也是形数。音律的和谐便是数学的和谐,甚至是宇宙的和谐。在毕达哥拉斯看来,数与数之间的比例关系操纵的不仅仅是音乐世界,还有世上一切具有美感的事物。比例与均衡控制着音乐的美、体格的美和数学的美。了解自然就是了解数学中的比例关系。
由此毕达哥拉斯学派及后来的古希腊数学家花费了许多精力挖掘数字比例的性质。最终他们将数之间的比例关系划分为10类,如调和中项(harmonic mean)等,其中的一个类别里有世上最“美丽”的一个比例——黄金比例。
未完待续.


