穿针引线法解一元高次不等式

穿针引线法

求一元高次不等式的解集

【方法介绍】

简单的一元高次不等式，主要通过分析对应函数的图象解决，常称为穿针引线法或数轴标根法、序轴标根法、根轴法，其步骤如下：

1)、将 $f(x)$ 最高次项的系数化为正.

2)、将 $f(x)$ 分解为若干个一次因式的积或二次不可分解因式的积，然后求出 $f(x)=0$ 的解，并在数轴上标出.(原不等式包含 "$=$ " 时用实心点；不含 "$=$ " 时用空心圆圈).

3)、自数轴正方向起，用曲线从右至左、自上而下依次由各解穿过数轴.

用曲线经各解穿数轴时，遵循 “寄过偶不过” 的原则，即对应因式的次数是寄数就穿过，为偶数则穿而不过。例如不等式

$(x-a)(x-b)^2$ $(x-c)$ $\geqslant 0$ （$c>b>a$ ）时，作图如下图：

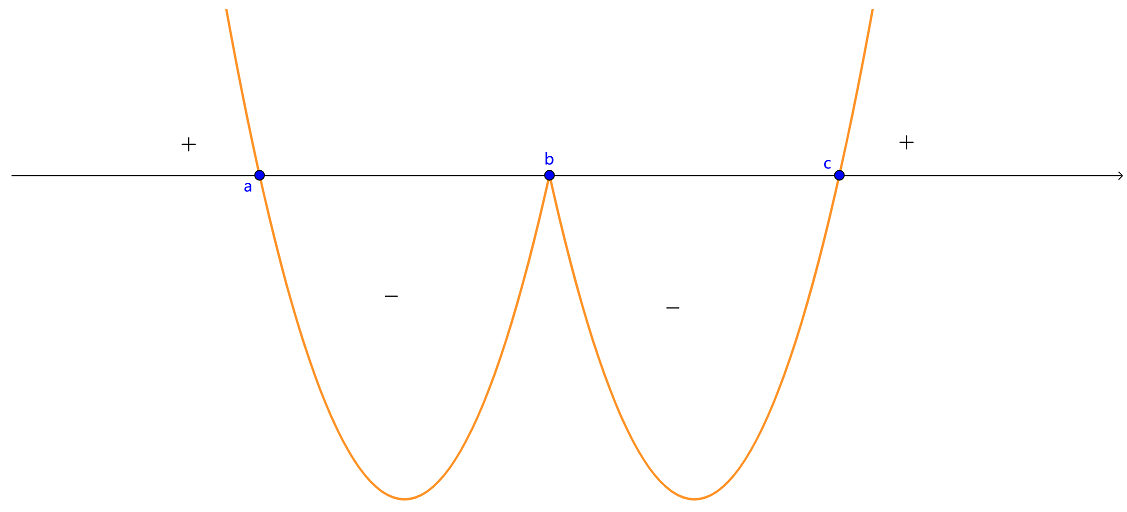
由于$(x-b)^2$ 项是偶数次，所以b这个根穿而不过.

4)、记数轴上方为正，下方为负，根据不等号写出解集.

用此方法需要注意两点，一是区点的端点能否取到，二是各因式中最高次项系数必须为正.

【例】

求不等式 

$(x^2-1)(x^3-1)$$(x^2-5x+6)$ $\leqslant 0$

的解集.

【解】

对原式因式分解得到

$(x-1)(x+1)(x-1)$$(x^2+x+1)$$(x-2)(x-3)$ $\leqslant 0$

$(x+1)(x-2)$$(x-3)(x-1)^2$ $(x^2+x+1)$$\leqslant 0$

计算

$(x+1)(x-2)$$(x-3)(x-1)^2$ $(x^2+x+1)$$=0$

的根

由于 $x^2+x+1$ 无实根，不用处理，其它几个根为，$-1,1,2,3$ , 将根标到数轴上并从右上开始穿线，注意偶次方因式 $(x-1)^2$ 的根 $1$ 不要穿过，得到下图:

题目要求小于等于0，所以解集为：

$\{x | x \leqslant -1$ 或 $x =1$ 或 $2 \leqslant x \leqslant 3$ $\}$