青羽讲数学史(三)
青羽讲数学史(三)
数学长征,青羽
于是,博物学家们注意到,一只跳蚤,其身上暗伏着更小的跳蚤,以它为猎物,它们的身上又有更小的跳蚤,伺机张口咬噬,如此往复,便是无限……
——乔纳森·斯威夫特《诗歌:狂想曲》
第二章 第一次数学危机——与无限的首次相会

一 ,无限、虚无与西方世界
毕达哥拉斯的核心思想是西方哲学体系的中心支柱:数是万物的本源;各行星在天球中有序运行,和谐旋律也随之而起。但是,在这些天体之外呢?是否有更多、更巨大的天体?或者说,位于运行轨道最外围的那颗行星是否就是宇宙的尽头?(古希腊人认为地球是宇宙的中心,日月众星皆绕地球运转。)

亚里士多德和后来的哲学家均坚称,不可能存在无限数量的嵌套天体。在其哲学观念下,“无限”这一概念完全被弃置一旁。亚里士多德认为,数学家“既不需要也用不到无限”。也许“无限”的概念会潜匿于数学家的思想深处,比如,将线条划分成无限多的小段,但没有人能真正做到这一点,所以,无限在现实生活中是不存在的。
亚里士多德将无限弃置一旁,并轻描淡写道“无限只不过是人类思维的构想。”
但是,由于芝诺这位在当时被评价为“最讨人厌”的哲学家,“无限”已悄然侵蚀西方思想的根基。
二,芝诺——希腊人不愿面对的梦魇
芝诺生于公元前490年左右,当时波斯战争刚刚打响,这是一场东方与西方的大规模开战。古希腊人也许能够战胜波斯人,可古希腊哲学却永远不可能征服芝诺——因为芝诺提出了一个悖论,在古希腊哲学家看来,这个逻辑上的难题相当棘手,甚至比希帕索斯提出的根号2危机更为致命。
芝诺提出,世界无一物处于运动的状态。这一说法无疑是荒唐的,只需要在房间里踱上几步便可驳斥。但即使每个人都知道这个观点的荒谬,但没有一个人能够从芝诺的论述中找出一丝的裂隙瑕疵。他提出的这个悖论困扰了古希腊的哲学家以及他们的后来者,在近千年的岁月里,这个逻辑谜题如梦魇般纠缠着各大数学家。
芝诺提出了许多关于运动的悖论,其中最著名的是“阿基里斯跑不过乌龟。”(阿基里斯是古希腊神话中跑得最快的神,为简化,下文仅简称为神。)他证明了,速度飞快的神永远也追不上动作迟缓、但比他先一步出发的乌龟。
说的具体些,假设神的速度是1米每秒,乌龟的速度是0.5米每秒,但起跑时乌龟在神的前方1米处。
神起步追赶,仅1秒钟就到达了乌龟的出发点,但在这一秒钟里,乌龟也在向前移动,前进了0.5米。没关系,神的速度很快,在0.5秒后又到了乌龟之前的位置,可这0.5秒内乌龟也前进了0.25米。神再花了0.25秒去追赶,但乌龟又前进了0.125米……
这个过程中,神的脚步未歇,但乌龟总能制造出无穷多个起点,且在起点与神之间制造出一个距离。不管这个距离有多短,是0.125米还是0.0625米还是更短,只要乌龟不停地奋力向前爬,神就永远追不上乌龟,因为乌龟总是先他一步。
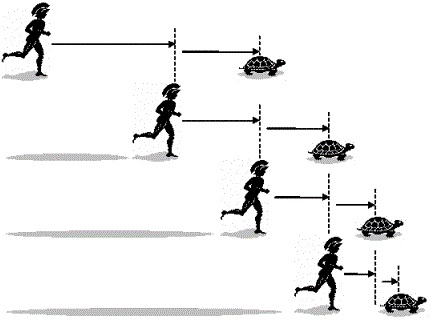
我们都清楚,在现实世界里,神肯定能追上乌龟,但芝诺的论证结果却截然相反。当时的哲学家无法驳倒这个悖论,他们无法从芝诺的数学论述中挑出一丝错处。
逻辑是哲学家手中的主要武器,但对于这个悖论,逻辑似乎无能为力。芝诺的这条逻辑链环环相扣,且每一环都无懈可击。但若环环相扣的论证都是正确的,为什么最后推导出来的结果会是这般荒谬呢?
这个问题彻底难住了古希腊人,但它们其实已经捕捉到了这团迷雾的源头:无限。 芝诺悖论的核心就是无限:芝诺将连续运动过程分割成无穷多的小段间隔,由于间隔的数量无限大,于是古希腊人就认为,尽管间隔距离越来越小,但神和乌龟总是在不停地运动。也就是说,在有限的时间里,追赶的过程永不停歇。
古人难以应付“无限”这个概念,好在现代数学已经掌握了其中的要领,经过数学界2400年的努力,今天的我们已可轻松准确地击中之诺悖论的阿基里斯之踵。
在刚才的问题中,我们可以把神追赶乌龟的过程分为无限多个阶段,分别是1,1/2,1/4...这个数列无穷无尽,没有终点,只是数字项的数值会越来越小,直到跨出他们掌握的数字范畴。
现代数学清楚地知道,这些累加项是有一个极限的,1,1/2,1/4,1/8,1/16...,最终趋近于0,这就是它们的极限。也就是说,这趟追赶的旅程是有终点的。一旦确认了终点的存在,人们自然也会发问,这个终点到底有多远?
实则将这个数列求和并非是难事:1+1/2+1/4+1/8+1/16+...+1/2^n+...,(2^n,即 )而随着神的跑动距离越来越小,越来越趋近于0,其累加结果就越来越趋近于2。这个过程昭示了:神需要走过无限多步才能跑完这一段有限的距离,但他所需的时间仅为2秒。
古希腊人无法识破这个小小的数字诡计,因为在他们的知识海洋里不具备极限的概念,但究其根源,还是在于他们对“无限”的不信任。
不过,西方世界对“无限”畏惧颇深,东方世界却欣然欢迎它的到来;“无限”在欧洲受尽冷眼,却在古印度、古中国的土地上大放异彩。
三,东方的极限思想
在《唱赞奥义书》中,有一句为“哪里有无限,哪里就有乐趣。有限毫无乐趣可言”在《梨俱吠陀》中,也有“在最远古的诸神时代,非存在中诞生了存在。”印度数学界永远欢迎“无限”,在他们的信仰中,虚无与无限占有重要地位。他们认为世界诞生于虚无之中,并且宇宙是广袤而无疆的。
在印度教中,创世之前的宇宙是一片虚无;创世之后,虚无依旧存在。世间万物始于虚无,人类的终极目标也是要归于虚无。有这样一个故事:死神向一个门徒讲述他关于灵魂的看法“灵魂、精神与自我都潜藏在人心深处,比最小的原子还要精细,又比广袤的空间还要浩瀚。”
“身体是灵魂的寄身之所,既能享受愉悦,又得承受苦痛,”神谕如此解释道,“一个人倘若完全受其身体支配,那么它永远都不可能摆脱轮回,进入超脱的自由之境。”但是,如果能将自身从肉体的虚妄中抽离出来,倾心感受与领悟灵魂的平静与虚无,那么人将得以解脱,灵魂将挣脱人欲的沉网,汇入群体意识的洪流。
可见,印度社会总在积极地探讨着有关无限与虚无的话题,因此其对无限的欣然接受也不足为奇了。
那么古中国呢?
中国思想家自春秋时期就有了对“无限”的认知,并在我国古代的文献中有所记载,其中最为著名的是《庄子·天下篇》中所记“一尺之棰,日取其半,万世不竭。”意思是一尺长的木头,每天仅砍它一半,那么永生永世也砍之不尽。
公元3世纪,中国数学家刘徽成功将极限思想应用于实践,其中最典型的方法即为“割圆术”。刘徽认为,割得越细,圆内接正多边形与圆的面积之差就越小,即“割之弥细,所失弥少,割之又割,以至于不可割,则与圆和体,而无所失矣。”
刘徽的割圆术是人类历史上首次将极限和无穷小分割引入数学证明,成为人类文明史中不朽的篇章。

刘徽
征求意见
本来数学史系列的第三章是打算讲文艺复兴时期数学家对一元三次方程根的求解过程探讨,一些文艺复兴时期数学家常进行的游戏,及其折射出的数学思想、数学方法。但本文末尾写到古中国对极限的认知,那么大家对中国古代的数学成就及数学思想是否感兴趣呢?还请大家在评论区留言,文艺复兴和古代中国二选一,作为我第三章的内容。


