进位制简介

进位制

进制

我们通常用的十进制，有两个特点：

（1）用0、1、2、3、4、5、6、7、8、9这十个数字（数码）表示；

（2）逢十进一.

除了十进制，还有其他的进位制. 例如南美的玛雅人采用二十进制；欧洲有过十二进制（1“打”表示12个）；我们现在的计时还在使用六十进制（60秒等于1分钟，60分钟等于1小时）；我国的旧称，是十六进制，1斤等于16两，所以“半斤八两”表示两个人实力相当，改用新称（十进制），就应当说“半斤五两”了.

二进制

二进制是十进制外最常用的进位制，是计算技术中广泛采用的一种数制.

二进制采用0、1两个数字（数码），逢二进一.

在十进制中，365中的3表示$3 \times 10^2$ ，6表示$6 \times 10^1$ . 同样，在二进制中，111中左起的第一个1表示$1 \times 2^2$ ，第二个1表示 $1 \times 2$ ，第三个1表示1.

为了避免混淆，$g$ 进制中的数常加一个括号，并在右下方加注一个$g$ ，例如二进制中的111，记为$(111)_2$ ，十进制的数仍然通常表示.

进制间转换

根据上面所说：

$(1111)_2$ $=$ $1 \times 2^3$ $+ 1 \times 2^2$ $+ 1 \times 2^1$ $+1$ $=15$

这就是二进制转为十进制的方法.

类似地，可以考虑$g$ 进制. 在$g$ 进制中，有$g$ 个数字，分别表示0、1、$\cdots$ 、$g-1$ ，在$g$ 大于10时需要自己制造几个新的数字，因为只有0到9这10个数字不够用. $g$ 进制“逢 $g$ 进一”.

一般地，$g$ 进制中的数可以写成 $(\overline{a_0 a_1 \cdots a_n})_g$ ，即

$(\overline{a_0 a_1 \cdots a_n})_g$ $=a_0 \times g^n$ $+a_1 \times g^{n-1}$ $+ \cdots$ $+ a_{n-1} \times g$ $+ a_n$

上述公式是$g$ 进制化十进制方法.

也说是说，$g$ 进制化十进制用乘法，反过来，十进制化$g$ 进制，用除法. 例如将十进制的2774化为八进制，作短除法运算：

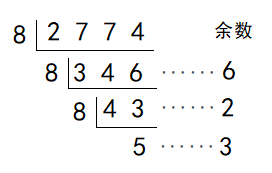
即

$2774 =$ $5 \times 8^3$ $+3 \times 8^2$ $+ 2 \times 8$ $+6$ $=(5326)_8$

也就是将余数从下往上写（5可以看作再除一次8所得的余数），便得出八进制中的数5326.